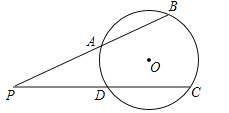
【题目】如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
(1)求证:PAPB=PDPC;
(2)若PA=![]() ,AB=
,AB=![]() ,PD=DC+2,求点O到PC的距离.
,PD=DC+2,求点O到PC的距离.
参考答案:
【答案】(1)证明见试题解析;(2)3.
【解析】
试题分析:(1)先连接AD,BC,由圆内接四边形的性质可知∠PAD=∠PCB,∠PDA=∠PBC,故可得出△PAD∽△PCB,再由相似三角形的对应边成比例即可得出结论;
(2)由PAPB=PDPC,求出CD,根据垂径定理可得点O到PC的距离.
试题解析:(1)连接AD,BC,∵四边形ABDC内接于⊙O,∴∠PAD=∠PCB,∠PDA=∠PBC,∴△PAD∽△PCB,∴![]() ,∴PAPB=PCPD;
,∴PAPB=PCPD;
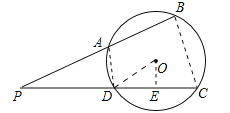
(2)连接OD,作OE⊥DC,垂足为E,∵PA=![]() ,AB=
,AB=![]() ,PD=DC+2,∴PB=16,PC=2DC+2,∵PAPB=PDPC,∴
,PD=DC+2,∴PB=16,PC=2DC+2,∵PAPB=PDPC,∴![]() ×16=(DC+2,第1题,2DC+2),解得:DC=8或DC=﹣11(舍去),∴DE=4,∵OD=5,∴OE=3,即点O到PC的距离为3.
×16=(DC+2,第1题,2DC+2),解得:DC=8或DC=﹣11(舍去),∴DE=4,∵OD=5,∴OE=3,即点O到PC的距离为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A﹣空气污染,B﹣淡水资源危机,C﹣土地荒漠化,D﹣全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:
关注问题
频数
频率
A
24
b
B
12
0.2
C
n
0.1
D
18
m
合计
a
1

根据表中提供的信息解答以下问题:
(1)表中的a= , b= .
(2)请将条形统计图补充完整;
(3)如果凯文所在的学校有3600名学生,那么根据凯文提供的信息估计该校关注“全球变暖”的学生大约多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示下列各数:0,–2.5,
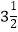 ,–2,+5,
,–2,+5, 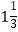 .并用“<”连接各数.比较大小: < < < < <
.并用“<”连接各数.比较大小: < < < < < -
科目: 来源: 题型:
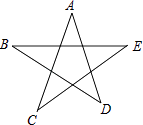
查看答案和解析>>【题目】如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
A.180°
B.150°
C.135°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=∠ABC=2∠A.

(1)求∠A的度数;
(2)若AB的垂直平分线MN交AC于D,连BD,求∠DBC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的的是( )
A.矩形的对角线互相垂直B.菱形的对角线相等
C.矩形的四个角不定相等D.正方形的对角线互相垂直且相等
相关试题

