【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE , 其中正确结论有( ) 
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】C
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
![]() ,
,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°(故②正确),
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故③正确).
设EC=x,由勾股定理,得
EF= ![]() x,CG=
x,CG= ![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°= ![]() x,
x,
∴AC= ![]() ,
,
∴AB= ![]() ,
,
∴BE= ![]() ﹣x=
﹣x= ![]() ,
,
∴BE+DF= ![]() x﹣x≠
x﹣x≠ ![]() x,(故④错误),
x,(故④错误),
∵S△CEF= ![]() x2,
x2,
S△ABE= ![]() x2,
x2,
∴2S△ABE= ![]() x2=S△CEF,(故⑤正确).
x2=S△CEF,(故⑤正确).
综上所述,正确的有4个,
故选:C.
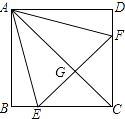
通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC,就可以得出AC垂直平分EF,设EC=x,BE=y,由勾股定理就可以得出x与y的关系,表示出BE与EF,利用三角形的面积公式分别表示出S△CEF和2S△ABE,再通过比较大小就可以得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.
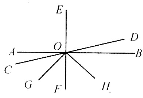
(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连结AE,则△ACE的周长是( )

A.8
B.10
C.14
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a6÷a3=a3
B.(a2)3=a8
C.(a﹣b)2=a2﹣b2
D.a2+a2=a4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点
,点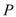 到
到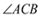 两边的距离相等,且
两边的距离相等,且 .
.(1)先用尺规作出符合要求的点
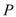 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;(2)设
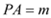 ,
,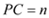 ,试用
,试用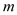 、
、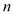 的代数式表示
的代数式表示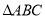 的周长和面积;
的周长和面积;(3)设
 与
与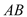 交于点
交于点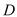 ,试探索当边
,试探索当边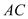 、
、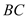 的长度变化时,
的长度变化时,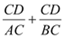 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式a2+a的值是5,则代数式2a2+2a+2013的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】x-2≤5,则x_________,写出此不等式的三个整数解______、______、______.
相关试题

