【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 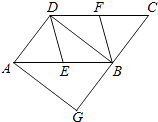
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE= ![]() AB,DF=
AB,DF= ![]() CD.
CD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF;

(2)证明:∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形.
【解析】(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC与点E,求证:PB=PE
分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N通过证明两三角形全等,进而证明两条线段相等.
学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.
解决问题:请你选择上述一种方法给予证明.
问题延伸:如图3,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.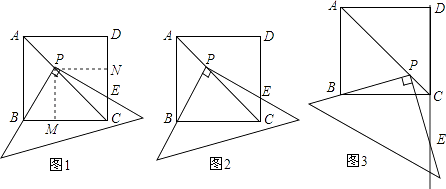
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽.甲、乙两个水槽中水的深度y(cm)与注水时间x(分)之间的关系如图2所示.根据图象解答下列问题:

(1)图2中折线ABC表示槽中水的深度与注水时间之间的关系.线段DE表示槽中水的深度与注水时间之间的关系.点B的纵坐标的实际意义是 .
(2)注水多长时间,甲、乙两个水槽中水的深度相同.
(3)若乙槽底面积为36cm2 , (壁厚不计),求乙槽中铁块的体积.
(4)若乙槽中铁块的体积为112cm3 , 则甲槽的底面积是cm2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,同位角相等”的题设是 , 结论是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a﹣2a=a
B.2a3a=6a
C.a2a3=a6
D.(3a)2=6a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3+2x>5的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

相关试题

