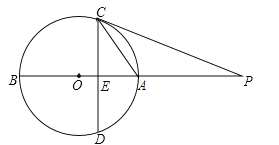
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且![]() =PEPO.
=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)3.
【解析】
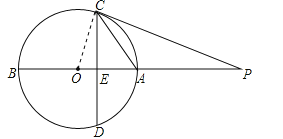
试题分析:(1)连结OC,如图,由![]() =PEPO和公共角可判断△PCE∽△POC,则∠PEC=∠PCO=90°,然后根据切线的判定定理可判断PC是⊙O的切线;
=PEPO和公共角可判断△PCE∽△POC,则∠PEC=∠PCO=90°,然后根据切线的判定定理可判断PC是⊙O的切线;
(2)设OE=x,则EA=2x,OA=OC=3x,证明△OCE∽△OPC,利用相似比可表示出OP,则可列方程3x+6=9x,然后解出x即可得到⊙O的半径.
试题解析:(1)证明:连结OC,如图,∵CD⊥AB,∴∠PEC=90°,∵![]() =PEPO,∴PC:PO=PE:PC,而∠CPE=∠OPC,∴△PCE∽△POC,∴∠PEC=∠PCO=90°,∴OC⊥PC,∴PC是⊙O的切线;
=PEPO,∴PC:PO=PE:PC,而∠CPE=∠OPC,∴△PCE∽△POC,∴∠PEC=∠PCO=90°,∴OC⊥PC,∴PC是⊙O的切线;
(2)解:设OE=x,则EA=2x,OA=OC=3x,∵∠COE=∠POC,∠OEC=∠OCP,∴△OCE∽△OPC,∴OC:OP=OE:OC,即3x:OP=x:3x,解得OP=9x,∴3x+6=9x,解得x=1,∴OC=3,即⊙O的半径为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为千米;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组或不等式组
(1)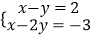
(2)解不等式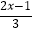 ﹣
﹣ 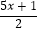 ≥1,把它的解集在数轴上表示出来.
≥1,把它的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】把点(2,﹣3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )
A.(5,﹣1)
B.(﹣1,﹣5)
C.(5,﹣5)
D.(﹣1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,D.E为圆上两点,C为圆外一点,且∠E+∠C=90°.
(1)求证:BC为⊙O的切线.
(2)若sinA=
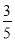 ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.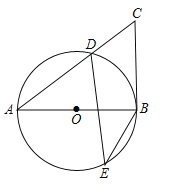
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的
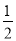 倍,纵坐标不变,得到函数y=2x的图象.
倍,纵坐标不变,得到函数y=2x的图象.类似地,我们可以认识其他函数.
(1)把函数
 的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数
的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数 的图象;也可以把函数
的图象;也可以把函数 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数
的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数 的图象.
的图象.(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移
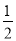 个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的
个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的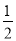 倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.(Ⅰ)函数
 的图象上所有的点经过④→②→①,得到函数 的图象;
的图象上所有的点经过④→②→①,得到函数 的图象;(Ⅱ)为了得到函数
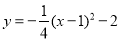 的图象,可以把函数
的图象,可以把函数 的图象上所有的点 .
的图象上所有的点 .A.①→⑤→③B.①→⑥→③C.①→②→⑥D.①→③→⑥
(3)函数
 的图象可以经过怎样的变化得到函数
的图象可以经过怎样的变化得到函数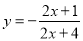 的图象?(写出一种即可)
的图象?(写出一种即可)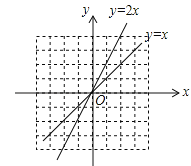
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
A.(﹣4,3)
B.(4,﹣3)
C.(﹣3,4)
D.(3,﹣4)
相关试题

