【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

参考答案:
【答案】(1)65°(2)证明见解析
【解析】
(1)由题意可得∠EAD=![]() ∠BAC=25°,再根据∠AED=90°,利用直角三角形两锐角互余即可求得答案;
∠BAC=25°,再根据∠AED=90°,利用直角三角形两锐角互余即可求得答案;
(2)由于DE⊥AB,易得∠AED=90°=∠ACB,而AD平分∠BAC,易知∠DAE=∠DAC,又因为AD=AD,利用AAS可证△AED≌△ACD,那么AE=AC,DE=DC,根据线段垂直平分线的判定定理即可得证.
(1)∵AD平分∠BAC,∠BAC=50°,
∴∠EAD=![]() ∠BAC=25°,
∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=90°-∠EAD=90°-25°=65°;
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又AD平分∠BAC,
∴∠DAE=∠DAC,
又∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,DE=DC
∴点A在线段CE的垂直平分线上,点D在线段CE的垂直平分线上,
∴直线AD是线段CE的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45°,则△EDF的周长等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细观察图中等边三角形图形的变化规律,写出你发现关于等边三角形内一点到三边距离的数学事实:_____________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等腰三角形,
是等腰三角形, ,
, .
. 尺规作图:作
尺规作图:作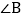 的角平分线BD,交AC于点
的角平分线BD,交AC于点 保留作图痕迹,不写作法
保留作图痕迹,不写作法 ;
; 判断
判断 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形
 中,
中, ,求
,求 的度数.
的度数.(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形 中,设
中,设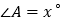 ,当
,当 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣1)2016+x0﹣ +
+ 
(2) ÷
÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,已知A(3,0),B(0, 4).
(I)求点C的坐标;
(Ⅱ)求经过点C,D两点的一次函数的解析式.

相关试题

