【题目】如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,且∠A=∠PDB.
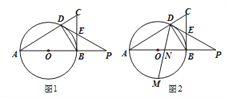
(1)求证:PD是⊙O的切线;
(2)如图2,点M是![]() 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A=![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)如图,作辅助线;要证明PD是⊙O的切线,只要证明∠PDO=90°,运用切线的判定定理,即可解决问题.
(2)如图,直接求出![]() 的值,非常困难;因此,需要作辅助线,构造相似三角形;运用已知条件tan∠A=
的值,非常困难;因此,需要作辅助线,构造相似三角形;运用已知条件tan∠A=![]() ,结合图形,联想勾股定理,设出BD=x,求出AB的长度;进而求出DF的长度;运用△OMN∽△FDN,得到
,结合图形,联想勾股定理,设出BD=x,求出AB的长度;进而求出DF的长度;运用△OMN∽△FDN,得到![]() ,即可解决问题.
,即可解决问题.
试题解析:(1)连结OD;
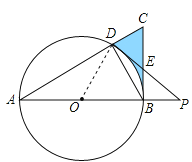
∵AB是⊙O的直径,
∴∠ADB=90°,OA=OB,∠A+∠ABD=90°;
又∵OA=OB=OD,
∴∠ADO=∠A,∠BDO=∠ABD;
又∵∠A=∠PDB,
∴∠PDB+∠BD0=90°,
即∠PDO=90°,且D在圆上,
∴PD是⊙O的切线.
(2)连结OM,过D作DF⊥AB于F;
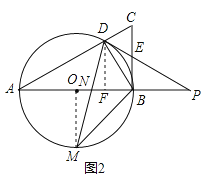
∵点M是![]() 的中点,
的中点,
∴OM⊥AB;设BD=x,
∵tan∠A=![]() ,
,
∴AD=4x;由勾股定理得:
AB= ![]() ;
;
由三角形的面积公式得: ![]() ADBD=
ADBD=![]() ABDF,
ABDF,
∴DF=![]() x;
x;
∵OM∥DF,
∴△OMN∽△FDN,
∴![]() ,DF=
,DF=![]() x,OM=
x,OM=![]() x,
x,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣1=2(x+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A.16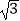
B.16
C.8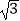
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】若3是关于方程x2-5x+c=的一个根,则这个方程的另一个根是( )
A.-2B.2C.-5D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.求山峰的高度CF(结果保留根号)
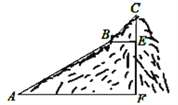
-
科目: 来源: 题型:
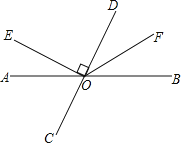
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
(1)图中除直角外,请写出一对相等的角吗: (写出符合的一对即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度数.(所求的角均小于平角)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,且c为有理数,则( )
A. ac>bc B. ac<bc C. ac2>bc2 D. ac2≥bc2
相关试题

