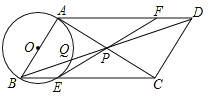
【题目】如图,在ABCD中,∠BAC=90°,对角线AC,BD相交于点P,以AB为直径的⊙O分别交BC,BD于点E,Q,连接EP并延长交AD于点F.
(1)求证:EF是⊙O的切线;
(2)求证:![]() =4BPQP.
=4BPQP.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)连接OE,AE,由AB是⊙O的直径,得到∠AEB=∠AEC=90°,根据四边形ABCD是平行四边形,得到PA=PC推出∠OEP=∠OAC=90°,根据切线的判定定理即可得到结论;
(2)由AB是⊙O的直径,得到∠AQB=90°根据相似三角形的性质得到![]() =PBPQ,根据全等三角形的性质得到PF=PE,求得PA=PE=
=PBPQ,根据全等三角形的性质得到PF=PE,求得PA=PE=![]() EF,等量代换即可得到结论.
EF,等量代换即可得到结论.
试题解析:(1)连接OE,AE,∵AB是⊙O的直径,∴∠AEB=∠AEC=90°,∵四边形ABCD是平行四边形,∴PA=PC,∴PA=PC=PE,∴∠PAE=∠PEA,∵OA=OE,∴∠OAE=∠OEA,∴∠OEP=∠OAC=90°,∴EF是⊙O的切线;
(2)∵AB是⊙O的直径,∴∠AQB=90°,∴△APQ∽△BPA,∴![]() ,∴
,∴![]() =PBPQ,在△AFP与△CEP中,∵∠PAF=∠PCE,∠APF=∠CPE,PA=PC,∴△AFP≌△CEP,∴PF=PE,∴PA=PE=
=PBPQ,在△AFP与△CEP中,∵∠PAF=∠PCE,∠APF=∠CPE,PA=PC,∴△AFP≌△CEP,∴PF=PE,∴PA=PE=![]() EF,∴
EF,∴![]() =4BPQP.
=4BPQP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
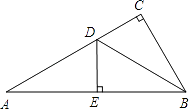
A.9cm
B.6cm
C.12cm
D.3cm -
科目: 来源: 题型:
查看答案和解析>>【题目】若0是一元二次方程(m﹣1)x2+6x+m2﹣1=0的一个根,则m取值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长40cm的绳子围成一个面积为64cm2的矩形.设矩形的一边长为xcm,则可列方程为_____.
-
科目: 来源: 题型:
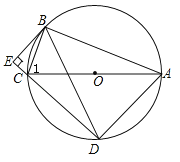
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
(1)∠1=∠BAD;
(2)BE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业前年缴税30万元,今年缴税36.3万元.那么该企业缴税的平均增长率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=mx+n与y=
 ,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )
,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )
A.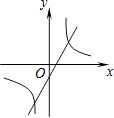
B.
C.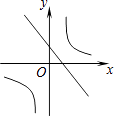
D.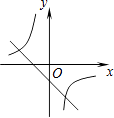
相关试题

