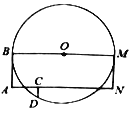
【题目】如图,![]() 是
是![]() 的直径,四边形
的直径,四边形![]() 是矩形,
是矩形,![]() 是
是![]() 上的点,
上的点,![]() ,与
,与![]() 交于点
交于点![]() ,己知
,己知![]() ,
,![]() 的半径为30.
的半径为30.
(1)求![]() 的长.
的长.
(2)连接![]() ,若将扇形
,若将扇形![]() 卷成一个圆锥,求这个圆锥底面半径的长.
卷成一个圆锥,求这个圆锥底面半径的长.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用矩形的性质以及锐角三角形函数关系,得出cos∠EOD的值进而求出∠EOD的度数,再利用弧长公式求出即可;
(2)设圆锥底面半径为r,结合OB=OD=30,∠BOD=60°,根据扇形弧长和圆锥底面周长的关系得出方程,解之即可.
(1)解:连接OD,BD,延长DC交BM于点E,
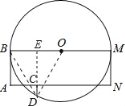
∵BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上一点,DC⊥AN,
∴DE⊥BO,
∵AC=15,
∴BE=EO=15,
∵DO=30,
∴![]() ,
,
∴∠EOD=60°,
∴![]() ;
;
(2)∵OB=OD=30,∠BOD=60°,设圆锥底面半径为r,
由题意可得:![]() ,
,
解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个函数给出如下定义:对于函数
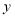 ,若当
,若当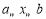 ,函数值
,函数值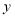 满足
满足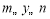 ,且满足
,且满足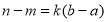 ,则称此函数为“
,则称此函数为“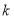 属和合函数”.
属和合函数”.例如:正比例函数
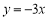 ,当
,当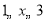 时,
时,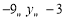 ,则
,则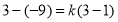 ,求得:
,求得: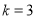 ,所以函数
,所以函数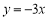 为“3属和合函数”.
为“3属和合函数”.(1)若一次函数
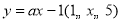 为“1属和合函数”,则
为“1属和合函数”,则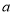 的值_________;
的值_________;(2)已知二次函数
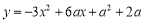 ,当
,当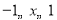 时,
时,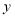 是“
是“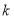 属和合函数”,则
属和合函数”,则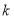 的取值范围_________.
的取值范围_________. -
科目: 来源: 题型:
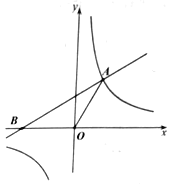
查看答案和解析>>【题目】已知:如图,一次函数
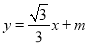 与反比例函数
与反比例函数 的图象在第一象限的交点为
的图象在第一象限的交点为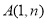 .
.
(1)求
 与
与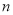 的值;
的值;(2)设一次函数的图像与
 轴交于点
轴交于点 ,连接
,连接 ,求
,求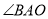 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x
1
2
3
4
5
6
7
成本(元/件)
56
58
60
62
64
66
68
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰
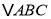 中,
中,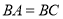 ,
,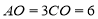 .动点
.动点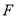 在
在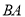 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从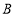 点出发向
点出发向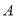 点移动,过
点移动,过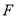 作
作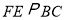 交
交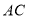 边于
边于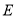 点,连结
点,连结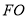 、
、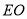 .设
.设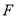 点移动的时间为
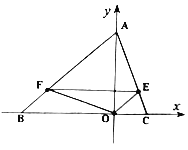
点移动的时间为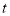 .
.
(1)求
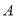 、
、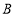 两点的坐标;
两点的坐标;(2)计算:当
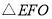 面积最大时,
面积最大时,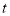 的值;
的值;(3)在(2)的条件下,边
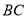 上是否还存在一个点
上是否还存在一个点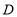 ,使得
,使得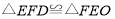 ?若存在,请直接写出
?若存在,请直接写出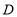 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,四边形 ABCD 是正方形,点 G 是 BC 上的任意一点,BF AG 于点 F,DE AG于点 E,探究 BF,DE,EF 之间的数量关系.第一学习小组合作探究后,得到DE–BF= EF,请证明这个结论;
(2)若(1)中的点 G 在 CB 的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时 BF,DE,EF 之间的数量关系;
(3)如图 ③ ,四边形 ABCD 内接于 ⊙O,AB=AD,E ,F 是AC 上的两点,且满足∠AED=∠BFA=∠BCD.试判断 AC,DE,BF 之间的数量关系,并说明理由.

相关试题

