搜索
【题目】如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，
D为AB边上一点.
(1)求证：△ACE≌△BCD
(2)若AD=6，BD=8，求DE的长.
参考答案：
【答案】（1）见详解；（2）10
【解析】
（1）根据两边夹角对应相等的两个三角形全等即可证明．
（2）只要证明∠EAD=90°，AE=BD=8，AD=6，根据勾股定理即可计算．
解：（1）∵△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，
∴AC=CB，EC=DC，∠ECA=∠DCB，
在△ECA和△DCB中，
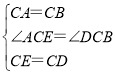
∴△ACE≌△BCD．
（2）∵△ACE≌△BCD，
∴AE=BD=8，∠CAE=∠B=45°，
∴∠EAD=∠EAC+∠CAB=90°，
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是边长为1的正方形，且DE＝
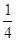，△ABF是△ADE的旋转图形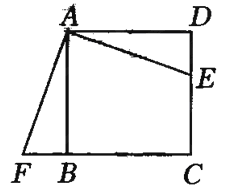
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）AF的长度是多少？
（4）如果连结EF，那么△AEF是怎样的三角形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L，M，D在AK的同旁，连接BK和DM，试用旋转的思想说明线段BK与DM的关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB=AC=AD，AD∥BC，
(1)求证：BD平分∠ABC；
(2)若∠C=78°，求∠D的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y1=-2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．
下列判断：
①当x＞0时，y1＞y2；
②当x＜0时，x值越大，M值越小；③使得M大于2的x值不存在；
④使得M=1的x值是
或
．其中正确的个数是（ ）A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.
（1）求证：OE是CD的垂直平分线.
（2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC和△DCB中，∠A＝∠D＝90°，AC＝BD，AC与BD相交于点O，限用无刻度直尺完成以下作图：
（1）在图1中作线段BC的中点P；
（2）在图2中，在OB、OC上分别取点E、F，使EF∥BC．
相关试题
