【题目】如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)点 E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.

参考答案:
【答案】(1)当E与F不重合时,四边形DEBF是平行四边形,理由见解析;(2)当运动时间t=4或28时,以D、E、B、F为顶点的四边形是矩形,理由见解析.
【解析】
解析:
(1)根据已知的AE=CF ,推出OE=OF ,根据平行四边形的性质得出OD=OB ,根据平行四边形的判定推出即可;
(2)根据矩形的性质得出BD=EF=12,得出方程16﹣0.5t﹣0.5t=12,求出即可;当E和F交换位置时得出方程0.5t﹣12+0.5t=16,求出即可.
(1)当E与F不重合时,四边形DEBF是平行四边形,
理由是:∵E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴OA﹣AE=OC﹣CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)当运动时间t=4或28时,以D、E、B、F为顶点的四边形是矩形,
理由是:分为两种情况:
①∵四边形DEBF是矩形,
∴BD=EF=12 cm,即AE=CF=0.5t cm,
则16﹣0.5t﹣0.5t=12,
解得:t=4;
②当E到F位置上,F到E位置上时,AE﹣AF=AC﹣CF,即0.5t﹣12+0.5t=16,
t=28,
即当运动时间t=4s或28s时,以D、E、B、F为顶点的四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
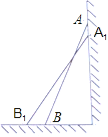
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=
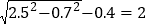
而A1B1=2.5,在Rt△A1B1C中,由
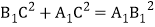 得方程 ,
得方程 ,解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目
测试成绩/分
甲
乙
丙
教学能力
85
73
73
科研能力
70
71
65
组织能力
64
72
84
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC长的2倍,则△ABC纸片扫过的面积为( )
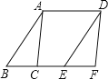
A.
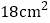 B.
B. 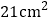 C.
C. 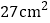 D.
D. 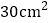
-
科目: 来源: 题型:
查看答案和解析>>【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况
 单位:元
单位:元
星期
一
二
三
四
五
每股涨跌
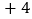
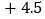
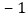
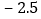
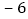
 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?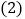 本星期内每股最低价多少元?
本星期内每股最低价多少元? 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB
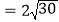 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )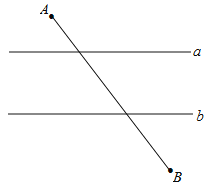
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
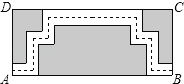
A.100米 B.99米 C.98米 D.74米
相关试题

