搜索
【题目】为更好宣传“开车不喝酒，喝酒不开车”的驾车理念，某市一家报社设计了如图1的调查问卷（单选），在随机调查了本市10000名司机中的部分司机后，统计整理并制作了如图2所示的统计图：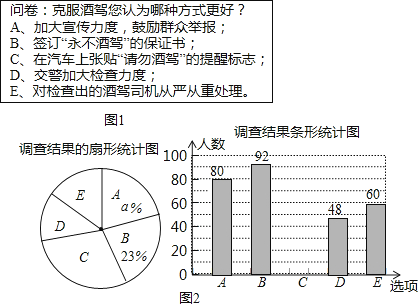
根据以上的信息解答下列问题：
（1）补全条形统计图，并计算扇形统计图中a= ．
（2）该市支持选项C的司机大约有多少人？
参考答案：
【答案】
（1）20
（2）
解：根据题意得：10000× 
=3000（人），
则该市支持选项C的司机大约有3000人
【解析】解：（1）由题意得：92÷23%=400（人），
则a%= 
×100%，即a=20；
所以答案是：（1）20
【考点精析】利用扇形统计图和条形统计图对题目进行判断即可得到答案，需要熟知能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况；能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．
正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正
边形ABCD…X”，请你作出猜想：当∠AMN=°时，结论AM=MN仍然成立．（直接写出答案，不需要证明）
图1 图2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰梯形OABC在平面直角坐标系中，如图A（1，2），B（3，2），C（4，0），则过点M（0，5）且把等腰梯形OABC面积分成相等两部分的直线解析式是
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，每个小方格的边长为1个单位长度，在第二象限内有横、纵坐标均为整数的A、B两点，点B（﹣2，3），点A的横坐标为﹣2，且OA=
． 
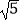（1）直接写出A点的坐标，并连接AB，AO，BO；
（2）画出△OAB关于点O成中心对称的图形△OA1B1 ， 并写出点A1、B1的坐标；（点A1、B1的对应点分别为A、B）
（3）将△OAB水平向右平移4个单位长度，画出平移后的△O1A2B2 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).
(1)在如图所示的平面直角坐标系画出该四边形；
(2)四边形ABCD的面积是________；
(3)四边形ABCD内（边界点除外)一共有_____个整点(即横坐标和纵坐标都是整数的点).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A信封中装有两张卡片，卡片上分别写着4cm、2cm，B信封中装有三张卡片，卡片上分别写着3cm、5cm、2cm．A、B信封外有一张写着5cm的卡片，所有卡片的形状、大小完全相同，现随机从两个信封中各取一张卡片，与信封外的卡片放在一起，用卡片上标明的数分别作为三条线段的长度．
（1）求这三条线段能组成三角形的概率（列举法、列表法或树形图法）；
（2）求这三条线段能组成直角三角形的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程．为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：
根据统计图中的信息，解答下列问题：
（
）求本次被调查的学生人数．（
）将条形统计图补充完整．（
）若该校共有
名学生，请估计全校选择体育类的学生人数．
相关试题
