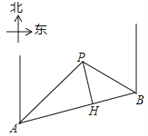
【题目】某条道路上通行车辆限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4).
≈1.4).
参考答案:
【答案】车辆通过AB段的时间在8.1秒以内,可认定为超速
【解析】分析:根据点到直线的距离的性质,构造直角三角形,然后利用解直角三角形的应用,解直角三角形即可.
详解:如图,由题意知∠CAB=75°,∠CAP=45°,∠PBD=60°,

∴∠PAH=∠CAB–∠CAP=30°,
∵∠PHA=∠PHB=90°,PH=50,∴AH=![]() =
=![]() =50
=50![]() ,
,
∵AC∥BD,∴∠ABD=180°–∠CAB=105°,∴∠PBH=∠ABD–∠PBD=45°,
则PH=BH=50,∴AB=AH+BH=50![]() +50,
+50,
∵60千米/时=![]() 米/秒,∴时间t=
米/秒,∴时间t=![]() =3+3
=3+3![]() ≈8.1(秒),
≈8.1(秒),
即车辆通过AB段的时间在8.1秒以内,可认定为超速.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=
 cm,且tan∠EFC=
cm,且tan∠EFC= ,那么该矩形的周长为________.
,那么该矩形的周长为________.
-
科目: 来源: 题型:
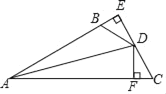
查看答案和解析>>【题目】如图,AD平分∠EAC,DE⊥AB于E,DF⊥AC于F,BD=CD,
(1)求证:BE=FC;
(2)已知AC=20,BE=4,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾天气持续笼罩我国大部分地区,困扰着广大市民的生活,口罩市场出现热销,小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售,销售完后共获利2700元,进价和售价如表:

(1)小明爸爸的商店购进甲、乙两种型号口罩各多少袋?
(2)该商店第二次以原价购进甲、乙两种型号口罩,购进甲种型号口罩袋数不变,而购进乙种型号口罩袋数是第一次的2倍,甲种口罩按原售价出售,而效果更好的乙种口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋乙种型号的口罩最多打几折?
-
科目: 来源: 题型:
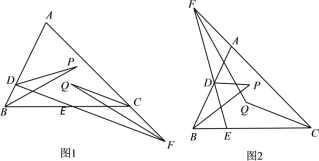
查看答案和解析>>【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在“清明小假期”举行促销活动,设立了一个可以自由转动的转盘进行摇奖活动,并规定顾客每购买200元商品,就可以获得一次转动转盘的机会,小明根据活动情况绘制了一个扇形统计图,如图所示.
(1)求每转动一次转盘所获得购物券金额的平均数;
(2)小明做了一次实验,他转了200次转盘,总共获得5800元购物券,他平均每转动一次转盘获得的购物券是多少元?
(3)请你说明上述两个结果为什么有差别?

-
科目: 来源: 题型:
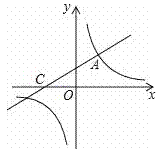
查看答案和解析>>【题目】如图,直线
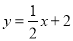 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C. (1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
相关试题

