【题目】如图,在平行四边形![]() 中,
中, ![]() 是
是![]() 的中点,延长
的中点,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
, ![]() .
.

(![]() )求证:
)求证: ![]() .
.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(![]() )证明见解析; (
)证明见解析; (![]() )
)![]() .
.
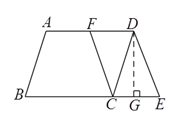
【解析】分析:(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
本题解析:
证明:(![]() )∵四边形
)∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
, ![]() ,
,
∵![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
(![]() )过点
)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() 且
且![]() ,
,
∴![]() ,
, ![]() ,
,
则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知等式x-3=5,两边同时________,得x=________,根据是________;
(2)已知等式4x=3x+7,两边同时________,得x=________,根据是________;
(3)已知等式
 ,两边同时________,得x=________,根据是________.
,两边同时________,得x=________,根据是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
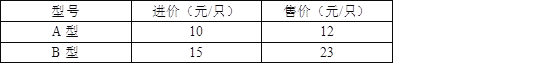
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用等式的性质解下列方程:
(1)
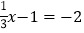 ;
;(2)10-4x=11;
(3)2x-4=3x+5;
(4)-2x+8=-12-7x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.增加6m2B.增加9m2C.减少9m2D.保持不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像分别与
的图像分别与 轴,
轴,  轴交于点
轴交于点 ,
,  ,点
,点 的坐标为
的坐标为 .
.
(
 )点
)点 的坐标为__________.
的坐标为__________.(
 )在第二象限内是否存在点
)在第二象限内是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题的结果正确的是( )
A. 3x+3y=6xy B. 16y2-7y2=9 C. -2(m-n)=-2m-2n D. 19a2b-9a2b=10a2b
相关试题

