【题目】如图,![]() 是边长为1的等边三角形,
是边长为1的等边三角形,![]() 为顶角
为顶角![]() 的等腰三角形,点
的等腰三角形,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,则
,则![]() 的周长为( )
的周长为( )
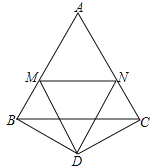
A.2B.3C.1.5D.2.5
参考答案:
【答案】A
【解析】
延长AC到E,使CE=BM,连接DE,求证△BMD≌△CED,可得∠BDM=∠CDE,进而求证△MDN≌△EDN可得MN=NE=NC+CE=NC+BM,即可计算△AMN周长.
如图所示,延长AC到E,使CE=BM,连接DE,
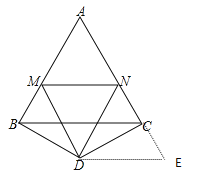
∵BD=DC,∠BDC=120°,
∴∠CBD=∠BCD=30°,
∵∠ABC=∠ACB=60°,
∴∠ABD=∠ACD=∠DCE=90°,
在△BMD和△CED中,
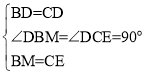
∴△BMD≌△CED(SAS),
∴∠BDM=∠CDE,DM=DE,
又∵∠MDN=60°,
∴∠BDM+∠NDC=60°,
∴∠EDC+∠NDC=∠NDE=60°=∠NDM,
在△MDN和△EDN中,
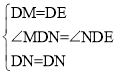
∴△MDN≌△EDN(SAS),
∴MN=NE=NC+CE=NC+BM,
所以△AMN周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=2.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(模型建立)(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E,求证:△BEC≌△CDA.
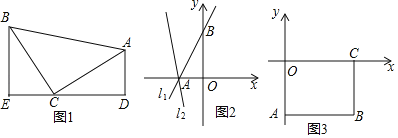
(模型应用)(2)①已知直线l1:y=
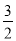 x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,﹣6),点A、C分别在坐标轴上,点P是线段BC上的动点,若△APD是以点D为直角顶点的等腰直角三角形,当点D在直线y=﹣2x+5上时,直接写出点D的坐标,并写出整个运动过程中点D的纵坐标n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】
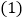 如图
如图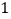 ,
,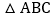 中,
中,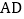 平分
平分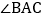 交
交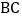 于点
于点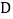 ,在
,在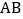 上截取
上截取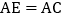 ,过点
,过点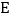 作
作 交
交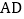 于点
于点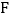 .求证:四边形
.求证:四边形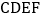 是菱形;
是菱形;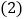 如图
如图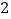 ,
,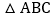 中,
中,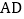 平分
平分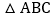 的外角
的外角 交
交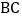 的延长线于点
的延长线于点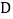 ,在
,在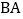 的延长线上截取
的延长线上截取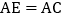 ,过点
,过点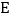 作
作 交
交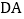 的延长线于点
的延长线于点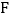 .四边形
.四边形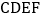 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.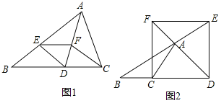
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,∠1=∠2,要使△ABC≌△ADE,还需添加的条件是_________.(只需填一个)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中,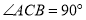 ,
,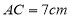 ,
,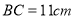 ,点
,点 从
从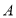 点出发沿
点出发沿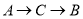 路径向终点
路径向终点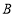 以
以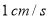 的速度运动,同时点
的速度运动,同时点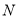 从
从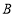 点出发沿
点出发沿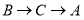 路径向终点
路径向终点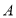 以
以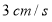 的速度运动,两点都要到达相应的终点时才能停止运动.分别过
的速度运动,两点都要到达相应的终点时才能停止运动.分别过 和
和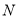 作
作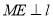 于
于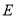 ,
, 于
于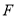 ,则当运动时间
,则当运动时间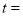 ____________
____________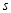 时,
时,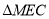 与去
与去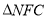 全等.
全等.
-
科目: 来源: 题型:
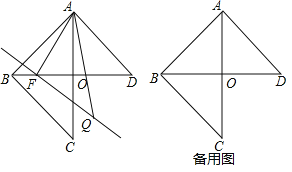
查看答案和解析>>【题目】已知在
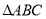 和
和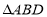 中,
中,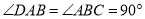 ,
,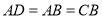 ,
,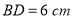 ,
,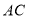 交
交 于点
于点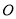 ,
,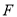 为线段
为线段 上一动点,以每秒
上一动点,以每秒 的速度从
的速度从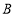 匀速运动到
匀速运动到 ,过
,过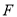 作直线
作直线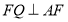 ,且
,且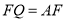 ,点
,点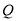 在直线
在直线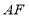 的右侧,设点
的右侧,设点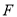 运动时间为
运动时间为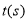 .
.
(1)当
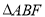 为等腰三角形时,
为等腰三角形时, ;
;(2)当
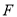 点在线段
点在线段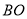 上时,过
上时,过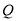 点作
点作 于点
于点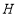 ,求证
,求证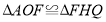 ;
;(3)当
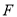 点在线段
点在线段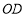 上运动的过程中,
上运动的过程中,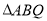 的面积是否变化?若不变,求出它的值.
的面积是否变化?若不变,求出它的值.
相关试题

