【题目】如图,四边形ABCD为矩形,E是BC延长线上一点,AE交CD于点G,F是AE上一点,并且AC=CF=EF,∠AEB=15°.
(1)求∠ACF的度数;
(2)证明:矩形ABCD为正方形.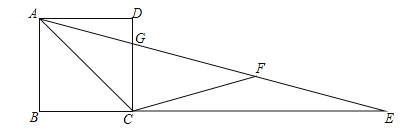
参考答案:
【答案】解:(1)∵四边形ABCD为矩形,
∴AD∥BC,∠D=90°,
∴∠DAG=∠AEB=15°,
∵CF=EF,
∴∠FCE=∠AEB=15°,
∴∠AFC=∠FCE+∠AEB=30°,
∵AC=CF,
∴∠FAC=∠AFC=30°,
∴∠ACF=18O°﹣∠FAC﹣∠AFC=120°;
(2)由(1)知∠DAG=15°,∠FAC=30°,
∴∠DAC=∠DAG+∠FAC=45°,
∵∠D=90°,
∴∠ACD=∠DAC=45°,
∴AD=CD,
∴矩形ABCD为正方形.
【解析】(1)利用矩形的性质可得∠DAG=∠AEB=15°,利用外角的性质和等腰三角形的性质可得∠AFC与∠CAF的度数,可得∠ACF;
(2)由∠DAG=15°,∠FAC=30°,易得∠DAC=45°,可得∠ACD=∠DAC=45°,由等腰三角形的判定可得AD=CD,由正方形的判定定理证得结论.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
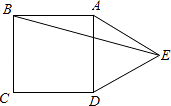
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD为菱形,其边长为6,
 ,点P在菱形的边AD、CD及对角线AC上运动,当
,点P在菱形的边AD、CD及对角线AC上运动,当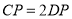 时,则DP的长为________.
时,则DP的长为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.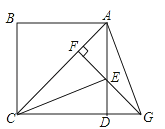
-
科目: 来源: 题型:
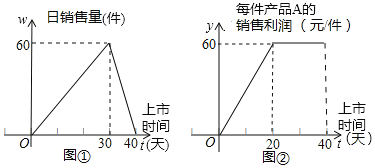
查看答案和解析>>【题目】某商场销售产品A,第一批产品A上市40天内全部售完.该商场对第一批产品A上市后的销售情况进行了跟踪调查,调查结果如图所示:图①中的折线表示日销售量w与上市时间t的关系;图②中的折线表示每件产品A的销售利润y与上市时间t的关系.
(1)观察图①,试写出第一批产品A的日销售量w与上市时间t的关系;
(2)第一批产品A上市后,哪一天这家商店日销售利润Q最大?日销售利润Q最大是多少元?(日销售利润=每件产品A的销售利润×日销售量)
-
科目: 来源: 题型:
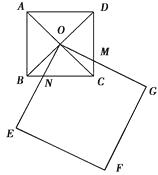
查看答案和解析>>【题目】如图四边形ABCD和四边形OEFG都是正方形,点O是正方形ABCD两对角线的交点,已知AB=2,EF=3,正方形OEFG绕点O转动,OE交BC上一点N,OG交CD上一点M.求四边形OMCN的面积.
-
科目: 来源: 题型:
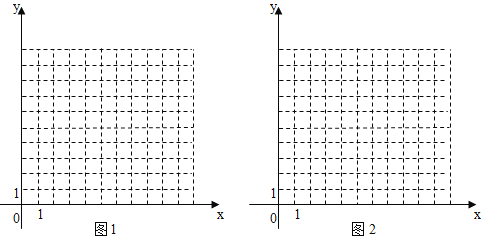
查看答案和解析>>【题目】在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm, 整点P从原点0出发,速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s)
可以得到整点P的坐标
可以得到整点P的个数
1
(0,1)(1,0)
2
2
(0,2)(1,1)(2,0)
3
3
(0,3)(1,2)(2,1)(3,0)
4
.
·
.
根据上表中的规律,回答下列问题:
(1)当整点P从点0出发4s时,可以得到的整点的个数为______个.
(2)当整点P从点O出发8s时,在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
(3)当整点P从点0出发______s时,可以得到整点(16,4)的位置.
相关试题

