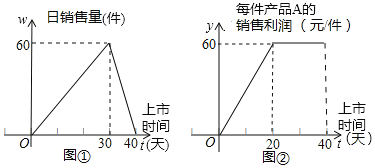
【题目】某商场销售产品A,第一批产品A上市40天内全部售完.该商场对第一批产品A上市后的销售情况进行了跟踪调查,调查结果如图所示:图①中的折线表示日销售量w与上市时间t的关系;图②中的折线表示每件产品A的销售利润y与上市时间t的关系.
(1)观察图①,试写出第一批产品A的日销售量w与上市时间t的关系;
(2)第一批产品A上市后,哪一天这家商店日销售利润Q最大?日销售利润Q最大是多少元?(日销售利润=每件产品A的销售利润×日销售量)
参考答案:
【答案】(1)当0≤t≤30时,日销售量w=2t;当30<t≤40时,日销售量w=﹣6t+240;(2)第一批产品A上市后30天,这家商店日销售利润Q最大,日销售利润Q最大是3600元.
【解析】
(1)根据题意和函数图象中的数据可以求得第一批产品A的日销售量w与上市时间t的关系;
(2)根据函数图象中的数据可以求得第一批产品A上市后,哪一天这家商店日销售利润Q最大,并求出Q的最大值.
解:(1)由图①可得,
当0≤t≤30时,可设日销售量w=kt,
∵点(30,60)在图象上,
∴60=30k.
∴k=2,即w=2t;
当30<t≤40时,可设日销售量w=k1t+b.
∵点(30,60)和(40,0)在图象上,
∴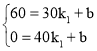 ,
,
解得,k1=﹣6,b=240,
∴w=﹣6t+240.
综上所述,日销售量w=![]() ;
;
即当0≤t≤30时,日销售量w=2t;当30<t≤40时,日销售量w=﹣6t+240;
(2)由图①知,当t=30(天)时,日销售量w达到最大,最大值w=60,
又由图②知,当t=30(天)时,产品A的日销售利润y达到最大,最大值y=60(元/件),
∴当t=30(天)时,日销售量利润Q最大,最大日销售利润Q=60×60=3600(元),
答:第一批产品A上市后30天,这家商店日销售利润Q最大,日销售利润Q最大是3600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD为菱形,其边长为6,
 ,点P在菱形的边AD、CD及对角线AC上运动,当
,点P在菱形的边AD、CD及对角线AC上运动,当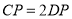 时,则DP的长为________.
时,则DP的长为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.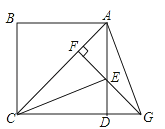
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形,E是BC延长线上一点,AE交CD于点G,F是AE上一点,并且AC=CF=EF,∠AEB=15°.
(1)求∠ACF的度数;
(2)证明:矩形ABCD为正方形.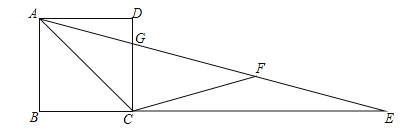
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD和四边形OEFG都是正方形,点O是正方形ABCD两对角线的交点,已知AB=2,EF=3,正方形OEFG绕点O转动,OE交BC上一点N,OG交CD上一点M.求四边形OMCN的面积.
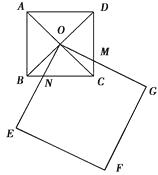
-
科目: 来源: 题型:
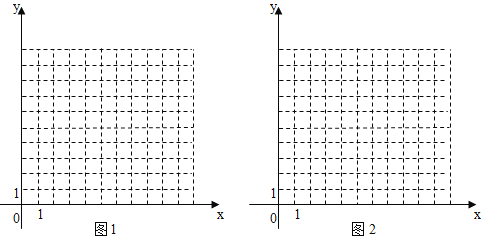
查看答案和解析>>【题目】在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm, 整点P从原点0出发,速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s)
可以得到整点P的坐标
可以得到整点P的个数
1
(0,1)(1,0)
2
2
(0,2)(1,1)(2,0)
3
3
(0,3)(1,2)(2,1)(3,0)
4
.
·
.
根据上表中的规律,回答下列问题:
(1)当整点P从点0出发4s时,可以得到的整点的个数为______个.
(2)当整点P从点O出发8s时,在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
(3)当整点P从点0出发______s时,可以得到整点(16,4)的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下
收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级
平均数
众数
中位数
方差
甲
4
3
乙
6
3.2
分析数据、推断结论
(1)该校初二乙班共有40名同学,你估计读6本书的同学大概有_____人;
(2)你认为哪个班同学寒假读书情况更好,写出理由.
相关试题

