【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为
轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为![]() .
.
(1)分别写出点P和Q坐标(用含t的代数式表示);
(2)①当点Q在BE之间运动时,设五边形PQBOD的面积为![]() (cm2),求y与t之间的函数关系式;
(cm2),求y与t之间的函数关系式;
②在①的情况下,是否存在某一时刻t,使PQ分四边形BODE两部分的面积之比为S△PQE:S五边形PQBOD=1:29?若存在,求出此时t的值;若不存在,请说明理由;
(3)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,当t为何值时,⊙P能与△ABO的一边相切?


参考答案:
【答案】(1)P(t,3),Q(8-![]() t,
t, ![]() t);
t);
(2)①![]() ②t=2,理由见解析
②t=2,理由见解析
(3)当t=![]() ,
, ![]() ,
, ![]() 时,⊙P可与△ABC的一边相切.
时,⊙P可与△ABC的一边相切.
【解析】试题分析:(1)利用直线的解析式首先求得直线与两坐标轴的交点坐标,然后利用三角形的中位线定理求得点P的纵坐标和点P的横坐标即可;(2)①由P作PH⊥AB得到△PHE∽△AOB,利用相似三角形对应边的比相等表示出PH,然后根据三角形的面积公式求解即可;②利用S△PQE:S五边形PQBOD=1:29列出方程求得t值即可;(3)分当⊙P与OB相切时、当⊙P与OA相切时和当⊙P与AB相切时三种情况分类讨论得到答案.
试题解析:
(1)P(t,3),Q(8-![]() t,
t, ![]() t);
t);
(2)
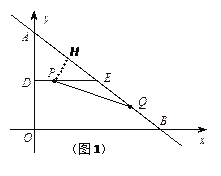
①如图1,P做PH⊥AB
△PHE∽△AOB
![]() ∴
∴![]()
∴![]()
S△PEQ =

S四边形DOBE=![]() ×3=18
×3=18
![]()
②![]() ×18 解得t=-
×18 解得t=-![]() (舍),t=2
(舍),t=2
(3)
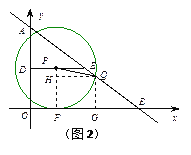
当⊙P与OB相切时,分别过点P、Q作PF、QG垂直于x轴,垂足为F、G,再过点Q作QH⊥PF于点H,如图2构造直角△PHQ,
此时,△BQG∽△BAO,BQ=2t,得QG=HF=![]() t,BG=
t,BG=![]() t,
t,
在Rt△PHQ中,PH2+HQ2=PQ2,得(3-![]() t)2+(8-t-
t)2+(8-t-![]() t)2=32,
t)2=32,
解得: t1=4(舍),t2=![]()
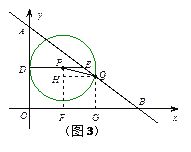
当⊙P与OA相切时,分别过点P、Q作PF、QG垂直于x轴,垂足为F、G,再过点Q作QH⊥PF于点H,如图3构造直角△PHQ,此时,△BQG∽△BAO,BQ=2t,得QG=HF=![]() t,BG=
t,BG=![]() t,
t,
在Rt△PHQ中,PH2+HQ2=PQ2,得(3-![]() t)2+(8-t-
t)2+(8-t-![]() t)2=t2,
t)2=t2,
解得: t1=![]() >4(舍),t2=
>4(舍),t2=![]()

当⊙P与AB相切时,如图4,此时, PE=4-t,EQ=2t-5,
由△EPQ∽△BAO,得![]() ,∴
,∴![]() ,解得: t=
,解得: t=![]()
∴当t=![]() ,
, ![]() ,
, ![]() 时,⊙P可与△ABC的一边相切.
时,⊙P可与△ABC的一边相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
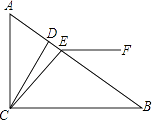
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是________(把所有你认为正确的序号都写上)
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“爱心小组”的九位同学为灾区捐款,捐款金额分别为20,10,15,15,18,17,12,14,11(单位:元).那么这组数据的中位数是( )
A. 18 B. 15 C. 14 D. 17
-
科目: 来源: 题型:
查看答案和解析>>【题目】将y=2x2的图象沿y轴向下平移3个单位,则得到的新图象所对应的函数表达式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,
 =
= 时,求DE的长.
时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式2x+a<3x的解为x>1,则a的值为( )
A.1
B.0
C.﹣1
D.﹣2
相关试题

