【题目】如图,在长方形纸片![]() 中,
中,![]() 点
点![]() 为
为![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠,刚好使点
折叠,刚好使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处.
处.

![]() 用尺规作图,在图上作出折叠线
用尺规作图,在图上作出折叠线![]() .以及点
.以及点![]() 的对称点
的对称点![]() (不写作法,但要保留作图痕迹,)
(不写作法,但要保留作图痕迹,)
![]() 求
求![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)BE=![]() .
.
【解析】
(1)作∠ADB的角平分线交AB于E,则DE即为折叠线;在DB上截取DF=DA可得点F的位置;
(2)根据勾股定理求出BD=26,则BF=16,设AE=EF=x,则BE=24-x,在Rt△BEF中,利用勾股定理构建方程求出x即可解决问题.
解:(1)如图所示,折叠线DE和点F即为所求;

(2)∵四边形ABCD是矩形,
∴AD=BC=10,∠A=90°,
∴BD=![]() ,
,
由折叠的性质得:AE=EF,AD=DF=10,
∴BF=26-10=16,
设AE=EF=x,则BE=24-x,
在Rt△BEF中,由勾股定理得EF2+BF2=BE2,
∴![]() ,
,
解得:![]() ,
,
∴BE=24-x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线
 与直线
与直线  在第二象限的交点,AB⊥
在第二象限的交点,AB⊥  轴于点B且S△ABO=
轴于点B且S△ABO=  .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长为1,点
的边长为1,点 与原点重合,
与原点重合, 在
在 轴正半轴上,
轴正半轴上, 在
在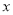 轴负半轴上,将正方形
轴负半轴上,将正方形 绕着点
绕着点 逆时针旋转
逆时针旋转 至
至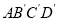 ,
, 与
与 相交于点
相交于点 ,则
,则 坐标为( )
坐标为( )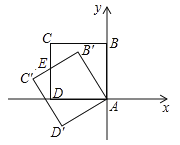
A.
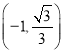 B.
B.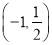 C.
C.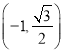 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB//CD,点E为平面内一点,BE⊥CE于E
(1)如图1,请直接写出∠ABE和∠DCE之间的数量关系
(2)如图2,过点E作EF⊥CD,垂足为F,求证:∠CEF=∠ABE
(3)如图3,在(2)的条件下,作EG平分∠CEF,交DF于点G,作ED平分∠BEF,交CD于D,连接BD,若∠DBE+∠ABD=180°,且∠BDE=3∠GEF,求∠BEG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中,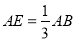 ,
,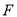 是对角线
是对角线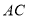 上的一个动点,若
上的一个动点,若 的最小值是10,则
的最小值是10,则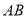 长为___________.
长为___________.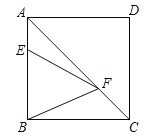
相关试题

