【题目】如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.

参考答案:
【答案】(1)证明见解析(2)4![]()
【解析】
(1) 要证OE⊥DC,可先证四边形OCED是菱形.由DE∥AC,CE∥BD,可得四边形OCED是平行四边形;又因为ABCD是矩形,所以OC=OD.有一组邻边相等的平行四边形是菱形.
(2)由(1) 得出△ODC是等边三角形,所以 DC=OD=OC=2 ,由四边形ABCD是矩形,得到AC=2CO=4, 在Rt△ADC中,由勾股定理得AD=2![]() ,再利用矩形面积公式即可解答.
,再利用矩形面积公式即可解答.
(1)证明:
∵DE∥AC,CE∥BD
∴DE∥OC,CE∥OD
∴四边形ODEC是平行四边形
∵四边形ODEC是矩形
∴OD=OC
∴四边形ODEC是菱形
∴OE⊥DC
(2)解:∵DE=2,由(1)知,四边形ODEC是菱形
∴OD=OC=DE=2
∵∠AOD=120°
∴∠DOC=60°
∴△ODC是等边三角形
∴DC=OD=OC=2
∵四边形ABCD是矩形
∴AC=2CO=4
在Rt△ADC中,由勾股定理得AD=2![]()
∴S矩形ABCD=2×2![]() =4
=4![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.

(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线
 与直线
与直线  在第二象限的交点,AB⊥
在第二象限的交点,AB⊥  轴于点B且S△ABO=
轴于点B且S△ABO=  .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形纸片
 中,
中, 点
点 为
为 上一点,将
上一点,将 沿
沿 折叠,刚好使点
折叠,刚好使点 落在对角线
落在对角线 上的点
上的点 处.
处.
 用尺规作图,在图上作出折叠线
用尺规作图,在图上作出折叠线 .以及点
.以及点 的对称点
的对称点 (不写作法,但要保留作图痕迹,)
(不写作法,但要保留作图痕迹,) 求
求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长为1,点
的边长为1,点 与原点重合,
与原点重合, 在
在 轴正半轴上,
轴正半轴上, 在
在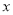 轴负半轴上,将正方形
轴负半轴上,将正方形 绕着点
绕着点 逆时针旋转
逆时针旋转 至
至 ,
, 与
与 相交于点
相交于点 ,则
,则 坐标为( )
坐标为( )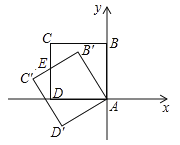
A.
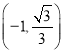 B.
B.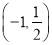 C.
C.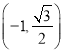 D.
D.
相关试题

