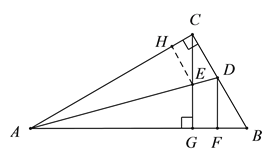
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED=
,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正确的是( )
;④CE=DF.正确的是( )

A. ①②④ B. ②③④ C. ①③ D. ①②③④
参考答案:
【答案】A
【解析】过点E作EH⊥AC,
∵AD平分∠CAB,CG⊥AB,∴EH=EG,
∴S△AEC:S△AEG= ![]() :
: ![]() =AC:AG,故②正确;
=AC:AG,故②正确;
∵∠ACE+∠BCG=90°,∠B+∠BCG=90°,
∴∠ACE=∠B,
∵∠CED=∠CAE+∠ACE,∠CDE=∠B+∠DAB,∠CAE=∠BAD,
∴∠CED=∠CDE,故①正确;
∴CE=CD,
又AE平分∠CAB,DF⊥AB,AC⊥BC,
∴CD=DF,∴CE=DF,故④正确;
无法证明∠ADF=2∠FDB,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店去年3至8月销售吐鲁番葡萄、哈密瓜的情况如下表:
3月
4月
5月
6月
7月
8月
吐鲁番葡萄(单位:百公斤)
4
8
5
8
10
13
哈密瓜(单位:百公斤)
8
7
9
7
10
7
(1)请你根据以上数据填写下表:
平均数/百公斤
方差
吐鲁番葡萄
8
9
哈密瓜
(2)请你根据上述信息,对这两种水果在去年3月份至8月份的销售情况进行分析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
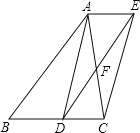
查看答案和解析>>【题目】如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F。
(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由;
(3)如果四边形ADCE是菱形,直接写出△ABC应满足的条件是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax﹣1的图象与反比例函数y=
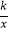 的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.
的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.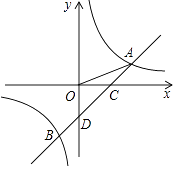
(1)求a,k的值及点B的坐标;
(2)直接写出不等式ax﹣1≥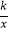 的解集;
的解集;
(3)在x轴上存在一点P,使得△POA与△OAC相似(不包括全等),请你求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)与x轴分别交于A(x1 , 0)、
B(x2 , 0)两点,直线y2=2x+t经过点A.
(1)已知A、B两点的横坐标分别为3、﹣1.
①当a=1时,直接写出抛物线y1和直线y2相应的函数表达式;
②如图,已知抛物线y1在3<x<4这一段位于直线y2的下方,在5<x<6这一段位于直线y2的上方,求a的取值范围;
(2)若函数y=y1+y2的图象与x轴仅有一个公共点,探求x2﹣x1与a之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
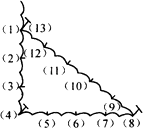
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.如果三角形两条边长的平方和等于第三边长的平方
D.如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
相关试题

