【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):请根据上表的内容解答下列问题:
表示立方米):请根据上表的内容解答下列问题:
(1)填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费___________元;
,则应收水费___________元;
(2)若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?
),则应收水费多少元?
价目表
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元/ |
(3)若该户居民![]() 、
、![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 、
、![]() 两个月共交水费多少元?(答案可含有
两个月共交水费多少元?(答案可含有![]() )
)
参考答案:
【答案】(1)8元;(2)(4a-12)元;(3)①-6x+68;② -2x+48;③36
【解析】
(1)不超过6m3,单价为2元.水费=单价×数量;
(2)水费=单价为2元的6m3的水费+单价为4元的超过6m3的水费;
(3)应分情况讨论:4月份不超过6m3,5月份10立方米以上;或4月份不超过6m3,5月份在6-10立方米之间;两个月都在6-10立方米之间.
(1)2×4=8(元);
(2)4(a6)+6×2=4a12,
∴应收水费为(4a12)元,
(3)因为5月份用水量超过了4月份,所以4月份用水量少于7.5m3.
①当4月份用水量少于5m3时,则5月份用水量超过10m3,
∴4,5两个月共交水费=2x+8(15x10)+4×4+6×2=6x+68(元);
②当4月份用水量大于或等于5m3但不超过6m3时,则5月份用水量不少于9m3但不超过10m3,
∴4、5两个月共交水费=2x+4(15x6)+6×2=2x+48(元);
③当4月份用水量超过6m3但少于7.5m3时,则5月份用水量超过7.5m3但少于9m3,
∴4,5两个月共交水费=4(x6)+6×2+4(15x6)+6×2=36(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是工人师傅用同一种材料制成的金属框架,已知
 ,
,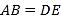 ,
, ,其中
,其中 的周长为24cm,
的周长为24cm, ,则制成整个金属框架所需这种材料的总长度为( )
,则制成整个金属框架所需这种材料的总长度为( )
A. 45cm B. 48cm C. 51cm D. 54cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用数轴解决问题:我们知道,若数轴上点
 表示的数是
表示的数是 ,点
,点 表示的数是
表示的数是 ,则
,则 、
、 两点间的距离记作
两点间的距离记作 ,
, .
.(1)若
 ,
, ,则
,则 = ;
= ; (2)若数轴上一点
 表示的数是
表示的数是 ,
, ,则
,则 = ;
= ;(3)若点
 表示的数是
表示的数是 ,已知
,已知 ,点
,点 在
在 的左边,
的左边, ,点
,点 在点
在点 的右边,
的右边, ,点
,点 以每秒
以每秒 的速度向右移动,同时点
的速度向右移动,同时点 、点
、点 分别以每秒
分别以每秒 、
、 的速度向左移动.设移动时间为
的速度向左移动.设移动时间为 秒,那么
秒,那么 是否有最小值?若有,求出最小值并写出此时
是否有最小值?若有,求出最小值并写出此时 的取值范围;若没有,请说明理由.
的取值范围;若没有,请说明理由. -
科目: 来源: 题型:
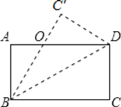
查看答案和解析>>【题目】如图所示,
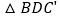 是将长方形纸牌ABCD沿着BD折叠得到的,图中
是将长方形纸牌ABCD沿着BD折叠得到的,图中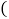 包括实线、虚线在内
包括实线、虚线在内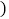 共有全等三角形______ 对
共有全等三角形______ 对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+b的图象与反比例函数y=
 (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1). 
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E.F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积为___________.

相关试题

