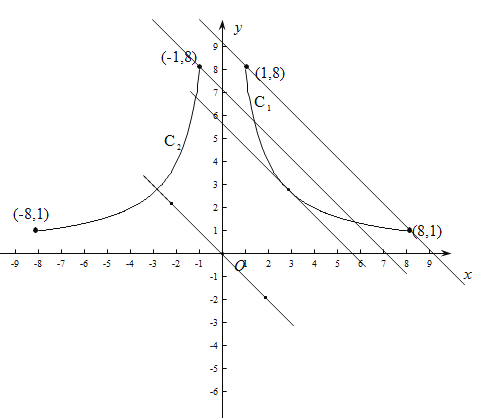
【题目】反比例函数y=![]() (1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
(1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
参考答案:
【答案】![]()
【解析】分析:作出大致图象,分两种情况讨论:①当直线y=-x+b与反比例函数y=![]() 只有一个交点时,解方程组得b=
只有一个交点时,解方程组得b=![]() ;②当直线y=-x+b过(-1,8)时,直线刚好与C1 ,C2有三个公共点,由此得到b的值,把此直线往上平移,直线与C2没有公共点,与C1有两个公共点,直到直线过(1,8),解得此时b的值,即可得出结论.
;②当直线y=-x+b过(-1,8)时,直线刚好与C1 ,C2有三个公共点,由此得到b的值,把此直线往上平移,直线与C2没有公共点,与C1有两个公共点,直到直线过(1,8),解得此时b的值,即可得出结论.
详解:如图,直线y=-x+b与直线l:y=-x平行.分两种情况讨论:
①当直线y=-x+b与反比例函数y=![]() 只有一个交点时,解方程组
只有一个交点时,解方程组 得:
得:![]() ,∴
,∴![]() ,∴△=b2-32=0,解得:b=±
,∴△=b2-32=0,解得:b=±![]() (负数舍去),∴b=
(负数舍去),∴b=![]() ,∴当b=
,∴当b=![]() ,直线y=-x+b与C1 ,C2一共只有两个公共点.
,直线y=-x+b与C1 ,C2一共只有两个公共点.
②当直线y=-x+b过(-1,8)时,直线刚好与C1 ,C2有三个公共点,此时8=1+b,解得:b=7,此时直线为y=-x+7,把此直线往上平移,直线与C2没有公共点,与C1有两个公共点,直到直线过(1,8),此时8=-1+b,解得:b=9.∴7<b≤9.
综上所述:b的取值范围是:b=![]() 或7<b≤9.
或7<b≤9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A. 2018 B. 2017 C. 55 D. 45
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )

A.
 B. 1 C.
B. 1 C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形腰长为2,有一个内角为80°,则它的底边长上的高为__.(精确到0.01,参考数据:sin50°≈0.766;sin80°≈0.985)
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.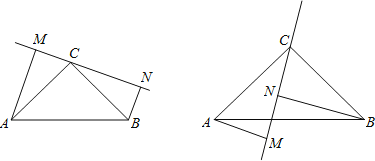
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

相关试题

