【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
参考答案:
【答案】
(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF
(2)解:∵四边形ACDE为菱形,AB=AC=1,
∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,
∴∠AEB=∠ABE=45°,
∴△ABE为等腰直角三角形,
∴BE= ![]() AC=
AC= ![]() ,
,
∴BD=BE﹣DE= ![]() ﹣1
﹣1
【解析】(1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;(2)由菱形的性质得到DE=AE=AC=AB=1,AC∥DE,根据等腰三角形的性质得∠AEB=∠ABE,根据平行线得性质得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判断△ABE为等腰直角三角形,所以BE= ![]() AC=
AC= ![]() ,于是利用BD=BE﹣DE求解.
,于是利用BD=BE﹣DE求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式;
(2)结合图像写出不等式
 的解集;
的解集;(3)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.

【答案】(1)y=
 ,y=-
,y=- x+7(2)0<x<2或x>12(3)点E的坐标为(0,5)或(0,9)
x+7(2)0<x<2或x>12(3)点E的坐标为(0,5)或(0,9)【解析】试题分析:(1)把点A的坐标代入反比例函数解析式,求出反比例函数的解析式,把点B的坐标代入已求出的反比例函数解析式,得出n的值,得出点B的坐标,再把A、B的坐标代入直线
 ,求出k、b的值,从而得出一次函数的解析式;
,求出k、b的值,从而得出一次函数的解析式;(2)设点E的坐标为(0,m),连接AE,BE,先求出点P的坐标(0,7),得出PE=|m﹣7|,根据S△AEB=S△BEP﹣S△AEP=10,求出m的值,从而得出点E的坐标.
解:(1)把点A(2,6)代入y=
 ,得m=12,则y=
,得m=12,则y= .
. 把点B(n,1)代入y=
把点B(n,1)代入y= ,得n=12,则点B的坐标为(12,1).
,得n=12,则点B的坐标为(12,1).由直线y=kx+b过点A(2,6),点B(12,1),
则所求一次函数的表达式为y=﹣
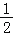 x+7.
x+7.(2)
 或
或 ;
;(3)如图,直线AB与y轴的交点为P,设点E的坐标为(0,m),连接AE,BE,则点P的坐标为(0,7).∴PE=|m﹣7|.
∵S△AEB=S△BEP﹣S△AEP=10,∴
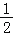 ×|m﹣7|×(12﹣2)=10.
×|m﹣7|×(12﹣2)=10.∴|m﹣7|=2.∴m1=5,m2=9.∴点E的坐标为(0,5)或(0,9).

【题型】解答题
【结束】
26【题目】太仓市为了加快经济发展,决定修筑一条沿江高速铁路,为了使工程提前半年完成,需要将工作效率提高25%。原计划完成这项工程需要多少个月?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(﹣2,0),C(2,2),过C作CB⊥x轴于B.

(1)如图1,△ABC的面积是 ;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标: ;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.

(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2 ,求⊙O 的半径长.
,求⊙O 的半径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.

(1)求该抛物线的函数关系式;
(2)设P(x,y),PD的长度为l,求l与x的函数关系式,并求l的最大值;
(3)当△ADP是直角三角形时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于反比例函数y=
 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.图象经过点(1,1)
B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称
D.当x<0时,y随x的增大而减小
相关试题

