搜索
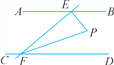
【题目】如图，已知AB∥CD，EF与AB，CD分别相交于点E，F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP＝50°，求∠EPF的度数．
参考答案：
【答案】70°
【解析】试题分析：由EP⊥EF，根据垂直的定义可得∠PEF＝90°，根据∠BEF＝∠BEP＋∠PEF求得∠BEF的度数；又因AB∥CD，根据平行线的性质可得∠BEF＋∠EFD＝180°，从而求得∠EFD的度数，再由角平分线的定义可得∠EFP的度数，最后根据三角形的内角和定理求得∠EPF的度数.
试题解析：
∵EP⊥EF，∴∠PEF＝90°.
∵∠BEP＝50°，
∴∠BEF＝∠BEP＋∠PEF＝140°.
∵AB∥CD，∴∠BEF＋∠EFD＝180°.
∴∠EFD＝40°.
∵FP平分∠EFD，∴∠EFP＝
∠EFD＝20°.
∵∠PEF＋∠EFP＋∠EPF＝180°，
∴∠EPF＝70°
-
科目： 来源： 题型：
查看答案和解析>>【题目】为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
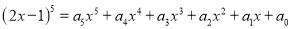,对于任意的x都成立求（1）a0的值
（2）a0﹣a1+a2﹣a3+a4﹣a5的值
（3）a2+a4的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 “囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．
（1）用含有x、y的代数式表示右图中“囧”的面积；
（2）当
时，求此时“囧”的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一楼房AB后有一假山，其坡度为i=1：
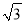，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC=25米，与亭子距离CE=20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）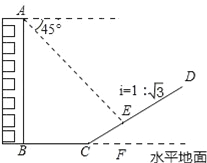
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，直线l：y=
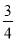x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y=
x2+bx+c经过点B，与直线l的另一个交点为C（4，n）．（1）求n的值和抛物线的解析式；
（2）点D在抛物线上，DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2），设点D的横坐标为t（0＜t＜4），矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；
（3）将△AOB绕平面内某点M旋转90°或180°，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，那么我们就称这样的点为“落点”，请直接写出“落点”的个数和旋转180°时点A1的横坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：有理数m所表示的点到点2距离3个单位，a、b互为相反数，且都不为零，c、d互为倒数．
（1）求m的值；
（2）求代数式：2（a+b）+（
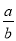﹣3cd）﹣m的值．
相关试题
