【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

参考答案:
【答案】(1)y=![]() t(0≤t≤
t(0≤t≤![]() ) (2)6小时
) (2)6小时
【解析】
(1) 将点![]() 代入函数关系式
代入函数关系式![]() , 解得
, 解得![]() , 有
, 有![]()
将![]() 代入
代入![]() , 得
, 得![]() , 所以所求反比例函数关系式为
, 所以所求反比例函数关系式为![]() ;
;
再将![]() 代入
代入![]() , 得
, 得![]() ,所以所求正比例函数关系式为
,所以所求正比例函数关系式为![]() .
.
(2) 解不等式![]() , 解得
, 解得![]() ,
,
所以至少需要经过6小时后,学生才能进入教室.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号热水器的容量为180升,设其工作时间为y分,每分的排水量为x升.
(1)写出y关于x的函数表达式和自变量x的取值范围;
(2)当每分钟的排水量为10升时,热水器工作多长时间?
(3)如果热水器可连续工作的时间不超过1小时,那么每分的排水量应控制在什么范围内?
-
科目: 来源: 题型:
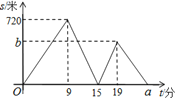
查看答案和解析>>【题目】小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;②小华的速度是小明速度的2.5倍;③a=24;④b=480.其中正确的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
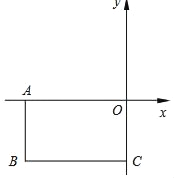
查看答案和解析>>【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=-2x+4,下列结论错误的是( )
A. 函数的图象与x轴的交点坐标是
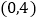
B. 函数值随自变量的增大而减小
C. 函数的图象不经过第三象限
D. 函数的图象向下平移4个单位长度得
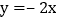 的图象
的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:
(1)如图1,已知点A,点B,点C,直线l及l上一点M,请你按照下列要求画出图形.
①画射线BM;
②画线段AC,并取线段AC的中点N;
③请在直线l上确定一点O,使点O到点A与点B的距离之和(OA+OB)最小;
(2)有5个大小一样的正方形制成如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,(只需添加一个符合要求的正方形即可,并用阴影表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
相关试题

