【题目】如图,在△ABC中,AB=AC,以AC为直径的半圆O交BC于点E,DE⊥AB,垂足为D.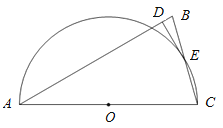
(1)求证:点E是BC的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)如果⊙O的直径为9,cosB=![]() , 求DE的长.
, 求DE的长.
参考答案:
【答案】
【解析】
(1)连接AE,根据等腰三角形的性质易证.
(2)相切,连接OE,证明OE⊥DE即可,根据三角形中位线定理证明.
(3)在Rt△ABE中,可由锐角三角函数定义可求BE的长;在Rt△BDE中,可由锐角三角函数定义和勾股定理可求DE的长.
【考点精析】关于本题考查的圆周角定理和直线与圆的三种位置关系,需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
分段数
频数
频率
60≤x<70
30
0.15
70≤x<80
60
n
80≤x<90
90≤x<100
20
0.1
合计
m
1
请根据以上图表提供的信息,解答下列问题:
(1)表中m的值为 , n的值为 ;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】试说明:用15块大小是4×1的矩形地砖和一块大小是2×2的正方形地砖能不能恰好铺盖一块大小是8×8的正方形地面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物小组观察一植物生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行x轴).
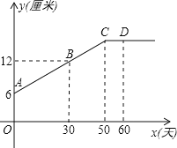
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的解析式,并求该植物最高长多少厘米?
-
科目: 来源: 题型:
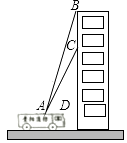
查看答案和解析>>【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国的发展与强大,中国文化与世界各国文化的交流与融合进一步加强.为了增进世界各国人民对中国语言和文化的理解,在世界各国建立孔子学院,推广汉语,传播中华文化.同时,各国学校之间的交流活动也逐年增加.在与国际友好学校交流活动中,小敏打算制做一个正方体礼盒送给外国朋友,每个面上分别书写一种中华传统美德,一共有“仁义礼智信孝”六个字.如图是她设计的礼盒平面展开图,那么“礼”字对面的字是( )
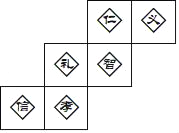
A. 仁 B. 义 C. 智 D. 信
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
相关试题

