搜索
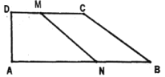
【题目】如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=26cm，DC=18cm ，AD=4cm，动点M以1cm/s的速度从点D向点C运动，动点N从点B以2cm/s的速度向点A运动点M、N同时出发，当其中一个动点到达端点时停止运动，另一个动点也随之停止运动，设动点运动时间为t(s)，四边形ANMD的面积y(
)，y关于x的函数解析式并写出定义域_____.
参考答案：
【答案】y=-2t+52，0＜t＜13.
【解析】
要能根据函数图象的性质和图象上的数据，分析得出函数的类型和所需要的条件，结合实际意义即可求出定义域．
解：∵在直角梯形ABCD中，DC∥AB，∠A=90，
∴四边形ANMD也是直角梯形，因此它的面积为：
（DM+AN）×AD，
∵DM=t，AN=26-2t，AD= 4；
∴四边形AMND的面积：y=（t+26-2t）×4=-2t+52．
∵当其中一个动点到达端点停止运动时，另一个动点也随之停止运动；
∴当N点到达A点时，2t=26，
解得：t=13；
∴自变量t的取值范围是：0＜t＜13．
故答案为：0＜t＜13.
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两家采摘园的圣女果品质相同，售价也相同，节日期间，两家均推出优惠方案，甲：游客进园需购买
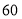元门票，采摘的打六折；乙：游客进园不需购买门票，采摘超过一定数量后，超过部分打折，设某游客打算采摘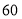
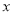千克，在甲、乙采摘园所需总费用为
、
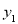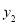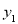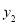元，、与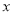之间的函数关系的图像如图所示.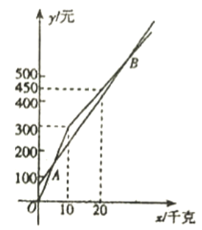
（1）分别求出
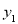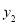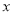、与之间的函数关系式；（2）求出图中点
、
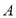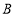的坐标； （3）若该游客打算采摘
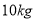圣女果，根据函数图像，直接写出该游客选择哪个采摘园更合算. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝k1x(x≥0)与双曲线y＝
(x＞0)相交于点P(2，4)．已知点A(4，0)，B(0，3)，连接AB，将Rt△AOB沿OP方向平移，使点O移动到点P，得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C，连接CP.(1)求k1与k2的值；
(2)求直线PC的解析式；
(3)直接写出线段AB扫过的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将函数y＝
(x－2)2＋1的图象沿y轴向上平移得到一条新函数的图象，其中点A(1，m)，B(4，n)平移后的对应点分别为点A′，B′，若曲线段AB扫过的面积为9(图中的阴影部分)，则新图象的函数表达式是__________.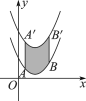
-
科目： 来源： 题型：
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地，在途中休息了-段时间后，仍按原速行驶他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段AB所示，
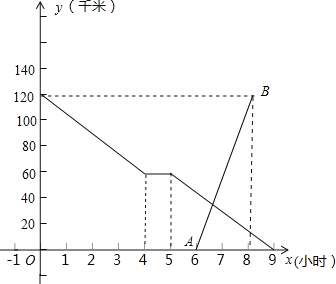
(1)小李到达甲地后，再经过 小时小张到达乙地；小张骑自行车的速度是 千米/小时；
(2)请你写出小李距乙地的距离y(千米)与时间x(小时)之间的函数关系(不要求写出定义域);
(3)若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇，则他出发的时间x应在什么范围?(直接写出答案)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD的周长是20 cm，以AB，AD为边向外作正方形ABEF和正方形ADGH，若正方形ABEF和ADGH的面积之和为68 cm2，那么矩形ABCD的面积是_______cm2．
-
科目： 来源： 题型：
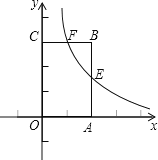
查看答案和解析>>【题目】如图，将一个长方形放置在平面直角坐标系中，
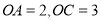，点
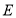是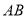
的中点，反比例函数图像过点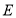且和
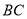相交于点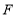
.
（1）求直线
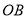和反比例函数的解析式；（2）求四边形
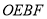的面积.
相关试题
