【题目】如图所示,在数轴上A点表示数aB点表示数![]() ,且a、b满足
,且a、b满足![]() ,
,
点A、点B之间的数轴上有一点C,且BC=2AC,
(1)点A表示的数为______,点B表示的数为______;则C点表示的数为______.
(2)若一动点P从点A出发,以3个单位长度/秒速度由A向B运动;同一时刻,另一动点Q从点C出发,以1个单位长度/秒速度由C向B运动,终点都为B点.当一点到达终点时,这点就停止运动,而另一点则继续运动,直至两点都到达终点时才结束整个运动过程.设点Q运动时间为t秒.
①经过______秒后,P、Q两点重合;
②点P与点Q之间的距离 PQ=1时, 求t的值.
![]()
参考答案:
【答案】(1)-3,9,1;(2)2秒;(3)![]() 或
或![]() 或7秒.
或7秒.
【解析】
(1)根据非负数的性质求出a、b的值即可;设C点表示的数为x,则-3<x<9,根据BC=2AC列出方程,解方程即可;
(2) ①根据路程=速度×时间可得AP=3t,CQ=t,根据AC=AP-CQ列方程即可求出t;
②分三种情况:点P在点Q的左边;t<4时,点P在点Q的右边;4<t<8时,点P到达点B,停止运动,此时QB=1.
(1)∵|2a+6|+|b-9|=0,
∴2a+6=0,b-9=0,
∴a=-3,b=9,
即点A表示的数为-3,点B表示的数为9;
设C点表示的数为x,则-3<x<9,根据BC=2AC,
得9-x=2[x-(-3)],
解得x=1.
即C点表示的数为1;
(2)根据题意得,
AC=AP-CQ
∴3t-t=3+1
解得,t=2;
(3)分三种情况:
如果点P在点Q的左边,由题意得
3t+1+8-t=12,解得t=![]() ;
;
如果t<4时,点P在点Q的右边,由题意得
3t-1+8-t=12,解得t=![]() ;
;
如果4<t<8时,点P到达点B,停止运动,此时QB=1,由题意得
8-t=1,解得t=7.
即当t=![]() 或
或![]() 或7秒时,点P与点Q之间的距离为1个单位长度.
或7秒时,点P与点Q之间的距离为1个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣
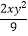 的系数为﹣2;
的系数为﹣2;(4)一个有理数不是整数就是分数
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为_______.(用a、b的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
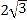 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点D在BC边上,将△ABD绕点A按逆时针方向旋转得到△ACE,连接DE,则图中与∠BAD相等的角,除∠CAE外,还有角 . (用三个字母表示该角)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中解为
 的方程是( )
的方程是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国邮政部门规定:国内平信
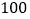 克以内(包括
克以内(包括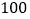 克)每
克)每 克需贴邮票
克需贴邮票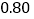 元,不足
元,不足 克重的以
克重的以 克计算;超过
克计算;超过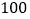 克的,超过部分每
克的,超过部分每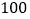 克需加贴
克需加贴 元,不足
元,不足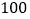 克的以
克的以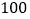 克计算.
克计算. 寄一封重
寄一封重 克的国内平信,需贴邮票多少元?
克的国内平信,需贴邮票多少元?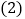 某人寄一封国内平信贴了
某人寄一封国内平信贴了 元邮票,此信重约多少克?
元邮票,此信重约多少克? 有
有 人参加一次数学竞赛,每份答卷重
人参加一次数学竞赛,每份答卷重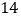 克,每个信封重
克,每个信封重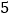 克,将这
克,将这 份答卷分装两个信封寄出,怎样装才能使所贴邮票金额最少?
份答卷分装两个信封寄出,怎样装才能使所贴邮票金额最少?
相关试题

