【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.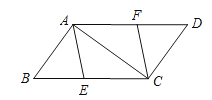
参考答案:
【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形.
(2)解:∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠BAC=90°,
∴∠3=90°﹣∠2,∠4=90°﹣∠1,
∴∠3=∠4,
∴AE=BE,
∴BE=AE=CE=![]() BC=5.
BC=5.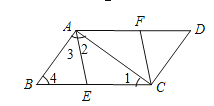
【解析】(1)利用平行四边形的性质得出AF∥EC,进而得出AF=EC,进而求出即可;
(2)利用菱形的性质以及三角形内角和定理得出∠1=∠2,进而求出∠3=∠4,再利用直角三角形的性质得出答案.
【考点精析】掌握平行四边形的判定与性质是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年广东梅州3分)若一个多边形的内角和小于其外角和,则这个多边形的边数是【 】
A.3 B.4 C.5 D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB=3cm,BC=2cm,那么AC=_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.

(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(参考数据:
 ≈1.73,sin37°≈
≈1.73,sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在学军活动中,一学生连续打靶5次,命中的环数如下:0,2,5,2,7这组数据的中位数与众数分别是(单位:环)( )
A.2,2B.5,2C.5,7D.2,7
-
科目: 来源: 题型:
查看答案和解析>>【题目】互为余角的两个角的和为_____度,互为补角的两个角的和为_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则7×6!的值为( )
A.42!B.7!C.6!D.6×7!
相关试题

