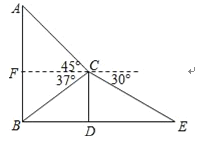
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.

(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
参考答案:
【答案】建筑物AB的高度约为11.67米
【解析】
试题分析:(1)由在Rt△CDE中,tan∠CED=![]() ,DE=8.65,∠CED=30°,即可求得答案;
,DE=8.65,∠CED=30°,即可求得答案;
(2)首先过点C作CF⊥AB于点F,然后在Rt△CBF中,求得FC,在Rt△AFC中,求得AF,继而求得答案.
试题解析:(1)在Rt△CDE中,tan∠CED=![]() ,DE=8.65,∠CED=30°,
,DE=8.65,∠CED=30°,
∴tan30°=![]() ,
,
解得:DC≈![]() =5,
=5,
∴建筑物CD的高度约为5米;
(2)过点C作CF⊥AB于点F.
在Rt△CBF中,tan∠FCB=![]() ,BF=DC=5,∠FCB=37°,
,BF=DC=5,∠FCB=37°,
∴tan37°=![]() ≈
≈![]() ,FC≈6.67,
,FC≈6.67,
在Rt△AFC中,∵∠ACF=45°,
∴AF=CF=6.67,
∴AB=AF+BF≈11.67,
∴建筑物AB的高度约为11.67米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.
(1)直接写出∠ADE的度数(用含α的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.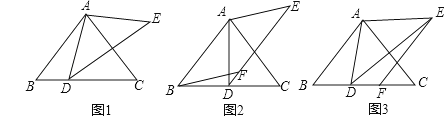
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年广东梅州3分)若一个多边形的内角和小于其外角和,则这个多边形的边数是【 】
A.3 B.4 C.5 D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB=3cm,BC=2cm,那么AC=_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.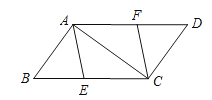
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在学军活动中,一学生连续打靶5次,命中的环数如下:0,2,5,2,7这组数据的中位数与众数分别是(单位:环)( )
A.2,2B.5,2C.5,7D.2,7
-
科目: 来源: 题型:
查看答案和解析>>【题目】互为余角的两个角的和为_____度,互为补角的两个角的和为_____度.
相关试题

