【题目】在解方程![]() x+
x+![]() (x﹣94)=35时,小明被难住.以下是小明、小丽、小飞同学的对话和解答过程,请你将其补充完整:
(x﹣94)=35时,小明被难住.以下是小明、小丽、小飞同学的对话和解答过程,请你将其补充完整:
小明:你俩只要帮我讲讲解此方程第一步的想法、依据就可以了.
小丽:解此方程的第一步,我观察到含有括号,我认为应先_____,依据是_____,就可以考虑合并同类项了.
小明利用小丽的想法写出了完整的解答过程如下:
小飞:解此方程的第一步还可以这样想,我观察到此方程含分母,我认为应先_____,在方程两边都_____,依据是_____.
小明利用小飞的想法写出了完整的解答过程如下:
参考答案:
【答案】去括号. 乘法分配律; 去分母 同时乘以4 等式的基本性质2
【解析】
两种方法求解方程一种是先去括号,依据是乘法分配律,接着合并同类项;另一种是先去分母,再方程两边都同时乘以4,依据是等式的基本性质2即可解题.
解:小丽:解此方程的第一步,我观察到含有括号,我认为应先去括号,依据是乘法分配律,就可以考虑合并同类项了.
![]() x+
x+![]() (x﹣94)=35,
(x﹣94)=35,
![]() x+
x+![]() x﹣
x﹣![]() ×94=35,
×94=35,
![]() x+
x+![]() x=
x=![]() ×94+35,
×94+35,
![]() x=
x=![]() ×94+35,
×94+35,
x=78;
小飞:解此方程的第一步还可以这样想,我观察到此方程含分母,我认为应先去分母,在方程两边都同时乘以4,依据是等式的基本性质2.
![]() x+
x+![]() (x﹣94)=35,
(x﹣94)=35,
2x+(x﹣94)=4×35,
2x+x﹣94=140,
3x=234,
x=78.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接“六一”国际儿童节,某童装品牌专卖店准备购进甲、乙两种童装,这两种童装的进价和售价如下表:
价格
甲
乙
进价(元/件)
m
m+20
售价(元/件)
150
160
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种童装共200件的总利润(利润=售价﹣进价)不少于8980元,且甲种童装少于100件,问该专卖店有哪几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
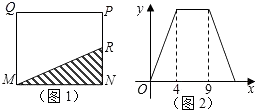
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y= 时,x=3
时,x=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:
(1)△ABD≌△CFD;
(2)BE⊥AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】饺子(如图1)源于古代的角子,饺子原名“娇耳”,相传是我国医圣张仲景首先发明的,距今已有一千八百多年的历史了.有一句民谣叫“大寒小寒,吃饺子过年.”包饺子时,将面团揉成长条状,后用刀切或用手揪成一个个小面团,这些小面团就是箕(jì)子(如图2).擀皮时,将箕子压扁后擀成圆形面皮,一个面箕子可以擀出一个饺子皮(如图3),就可以用来包饺子了.

中国北方,尤其是在京、津地区流行的一种面食﹣合子(如图4),含有团团圆圆的美好寓意.用两层饺子皮在中间加一层馅,就可以包成一个合子.北方有风俗曰:初一的饺子、初二的面、初三的合子往家转.
小亮的妈妈喜爱研究中华美食,自己动手经常给家人做出色香味俱佳的食品.妈妈在传承古人的做法的同时,也进行了加工创新.在每次包饺子临近结束时,如果饺子馅少了,饺子皮多了,这时妈妈会停止包饺子,改包合子,这样既不浪费食材,家人既吃到了饺子又吃到了合子.
这天,妈妈从厨房走到书房,对正在学习的小亮说:“妈妈刚才在厨房包饺子,结果面和多了,做了88个饺子箕,最后包了饺子和合子一共是81个.”
小亮说:“妈妈,我能用刚刚学到的列一元一次方程解应用题的知识和方法得出您包的饺子和合子分别是多少.”
请你写出小亮同学的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.若Rt△ABC为匀称三角形,且∠C=90°,AC=4,则BC= .
相关试题

