【题目】将一个正方体的表面全涂上颜色.
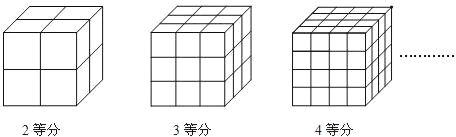
(1)如果把正方体的棱2等分,然后沿等分线把正方体切开,能够得到8个小正方体,设其中3面被涂上颜色的有a个,则a= ;
(2)如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到27个小正方体.设这些小正方体中有3个面涂有颜色的有a个,各个面都没有涂色的有b个,则a+b= ;
(3)如果把正方体的棱4等分,然后沿等分线把正方体切开,能够得到64个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= ;
(4)如果把正方体的棱n等分,然后沿等分线把正方体切开,能够得到 个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= .
参考答案:
【答案】(1)8;(2)9;(3)32;(4)![]() ,
,![]() .
.
【解析】
根据正方体的性质可发现顶点处的小方块三面涂色,除顶点外位于棱上的小方块两面涂色,涂色位于表面中心的一面涂色,处于正中心的没涂色.依此可得到(1)棱二等分时的所得小正方体表面涂色情况;(2)棱三等分时的所得小正方体表面涂色情况;(3)棱四等分时的所得小正方体表面涂色情况.(4)根据已知图形中没有涂色的小正方形个数得出变化规律进而得出答案.
解:(1)三面被涂色的有8个,故a=8;
(2)三面被涂色的有8个,各面都没有涂色的1个,a+b=8+1=9;
(3)两面被涂成红色有24个,各面都没有涂色的8个,b+c=24+8=32;
(4)由以上可发现规律:能够得到n3个小正方体,两面涂色c=12(n﹣2)个,各面均不涂色(n﹣2)3个,b+c=12(n﹣2)+(n﹣2)3.
故答案为:8,9,32,n3,12(n﹣2)+(n﹣2)3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,
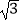 ≈1.7).
≈1.7).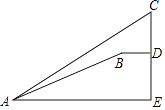
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论:①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.其中成立的个数是( )
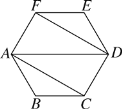
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AB=BC=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,点D的对应点为D′,连接D′B.若△D′BC为等边三角形,则DE=____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
相关试题

