【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.

(1)若AB=4,求弧CD的长.
(2)若弧BC=弧AD,AD=AP. 求证:PD是⊙O的切线.
参考答案:
【答案】(1)π;(2)见解析
【解析】试题分析:(1)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根据弧长公式即可得到结论;
(2)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD,求得∠ADP=![]() CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
试题解析:(1)连接OC,OD,
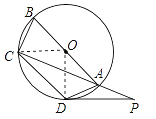
∵∠COD=2∠CAD,∠CAD=45°
∴∠COD=90°
∵AB=4 ∴![]()
∴![]() 的长
的长![]()
(2)∵![]() ∴∠BOC=∠AOD,
∴∠BOC=∠AOD,
∵∠COD=90°,∴∠AOD=![]()
∵OA=OD,∴∠ODA=∠OAD,
∵∠AOD+∠ODA+∠OAD=180° ∴∠ODA=![]() ,
,
∵AD=AP, ∴∠ADP=∠APD
∵∠CAD=∠ADP+∠APD, ∠CAD=45°,
∴∠ADP=![]() ∠CAD=22.5°,
∠CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°
又∵OD是半径,∴PD是⊙O的切线
-
科目: 来源: 题型:
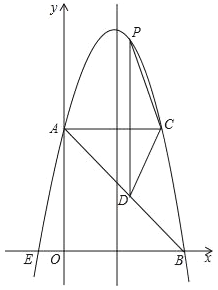
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是
A. 红红不是胜就是输,所以红红胜的概率为
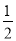
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为
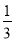
D. 娜娜胜的概率和两人出相同手势的概率一样
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
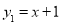 的图像与反比例函数
的图像与反比例函数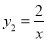 的图像交与
的图像交与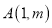 ,
,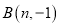 两点,过点A作
两点,过点A作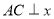 轴于点C,过点B作
轴于点C,过点B作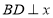 轴于点D,连接AO,
轴于点D,连接AO,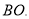 得出以下结论:
得出以下结论:①点A和点B关于直线
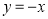 对称;
对称;②当
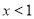 时,
时,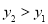 ;
;③
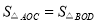 ;
; ④当
 时,
时, ,
, 都随x的增大而增大.
都随x的增大而增大.其中正确的是
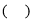
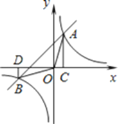
A.①②③B.②③C.①③D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=
 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(8)个图形有多少个正方体叠成( )

A.120个B.121个C.122个D.123个
相关试题

