【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(![]() 年—
年—![]() 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元![]() 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为![]() 、
、![]() 、
、![]() ,则三角形的面积
,则三角形的面积![]() (公式里的
(公式里的![]() 为半周长即周长的一半).
为半周长即周长的一半).
请利用海伦一秦九韶公式解决以下问题:
(![]() )三边长分别为
)三边长分别为![]() 、
、![]() 、
、![]() 的三角形面积为__________.
的三角形面积为__________.
(![]() )四边形
)四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 的面积为__________.
的面积为__________.
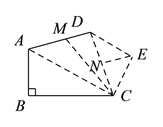
(![]() )五边形
)五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,五边形
,五边形![]() 的面积为__________.
的面积为__________.
参考答案:
【答案】(![]() )
)![]()
(![]() )
)![]()
(![]() )
)![]()
【解析】试题分析:(1)直接代入计算即可;
(2)连接AC,并示得AC的长度,再计算![]() 的面积,再得出四边形的面积;
的面积,再得出四边形的面积;
(3)将五边形分成四个三角形,再分别求出这四个三角形的面积,则求得五边形的面积.
试题解析:
(![]() )
)![]() ,
,
![]()
![]()
![]()
![]() .
.
(![]() )连接
)连接![]() .
.
∵![]() .
.
在![]() 中
中
∴![]()
![]()
![]() .
.
∵![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,
![]()
![]()
![]()
![]() .
.
∴![]() .
.

(![]() )连接
)连接![]() ,
,![]() .
.
∵![]() .
.
在![]() 中,
中,
![]()
![]() .
.
∵![]() ,
,
∴![]() .
.
![]()
![]()
![]() .
.
作![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
在![]() 中,
中,
![]()
![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]()
∴![]() ,
,
∴![]()
![]()
![]() .
.
作![]() 于
于![]() ,
,
设![]() ,则
,则![]() .
.
在![]() 中,
中,
![]() .
.
在![]() 中,
中,
![]()
∴![]()
∴![]() .
.
∴![]() .
.
∵![]()
∴![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的
 .
.(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
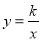 (k>0,x>0)的图象上,点D的坐标为(
(k>0,x>0)的图象上,点D的坐标为(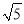 ,2).
,2).(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数
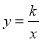 (k>0,x>0)的图象上时,求菱形ABCD平移的距离;
(k>0,x>0)的图象上时,求菱形ABCD平移的距离;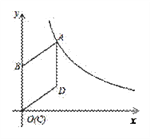
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=
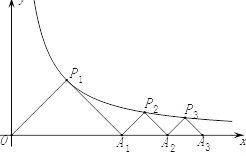
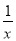 (x>0)的图象上,△P1OA1, △P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),
(x>0)的图象上,△P1OA1, △P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),(1)求点P1, P2, P3的坐标.
(2)猜想并直接写出点Pn的坐标(用含n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.

-
科目: 来源: 题型:
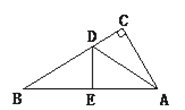
查看答案和解析>>【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
-
科目: 来源: 题型:
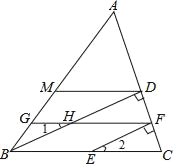
查看答案和解析>>【题目】如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°
(1)求∠GFC的度数:
(2)求证:DM∥BC.
相关试题

