【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.

参考答案:
【答案】(1)∠AEB=135°;(2)∠E=67.5°;(3)∠ABO为60°或45°.
【解析】试题分析:(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=∠OAB,∠ABE=∠ABO,由三角形内角和定理即可得出结论;
(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出∠OAB+∠OBA=90°,故∠PAB+∠MBA=270°,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知∠BAD=∠BAP,∠ABC=∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;
(3))由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=∠BAO,∠EOQ=∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
解:(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=∠BAP,∠ABC=∠ABM,
∴∠BAD+∠ABC=(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ﹣∠EAO=(∠BOQ﹣∠BAO)=∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°.
∴∠ABO为60°或45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】测试两种电子表的走时误差,做了如下统计,则这两种电子表走时稳定的是____.
平均数
方差
甲
0.4
0.026
乙
0.4
0.137
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,∠ACB=90°

(1)利用尺规作∠ABC 的平分线,交AC 于点O,再以O 为圆心,OC 的长为半径作⊙O(保留作图痕迹,不写作法);
(2)在你所作的图中,①判断AB 与⊙O 的位置关系,并证明你的结论;②若AC=12,tan∠OBC=
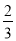 ,求⊙O 的半径。
,求⊙O 的半径。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.

(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
相关试题

