搜索
【题目】先化简，再求值：[（a+b）2﹣（a﹣b）2]a，其中a＝﹣1，b＝3．
参考答案：
【答案】4a2b，12．
【解析】
根据完全平方公式可以化简题目中的式子，然后将a、b的值代入化简后的式子即可解答本题．
解：[（a+b）2﹣（a﹣b）2]a
＝（a2+2ab+b2﹣a2+2ab﹣b2）a
＝4a2b，
当a＝﹣1，b＝3时，原式＝4×（﹣1）2×3＝12．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，假命题的是（ ）
A.两个等边三角形一定相似；
B.两个全等三角形一定相似；
C.有一个锐角相等的两个直角三角形一定相似；
D.有一个锐角相等的两个等腰三角形一定相似．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算﹣3+2＝（ ）
A.﹣1B.1C.﹣5D.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班40名同学的年龄情况如下表，则这40名同学的年龄的中位数是岁．
年齡/岁
14
15
16
17
人数
4
16
18
2
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明某一天放学从学校回家，如图，大致描述他回家过程中离家的距离S(千米)与所用时间t(分)之间的关系，下列说法错误的是（ ）
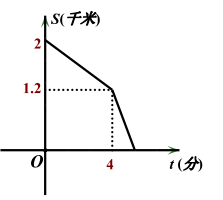
A.学校离家距离为2千米
B.前4分钟，小明平均速度为200米/分钟
C.骑了4分钟后，小明加快了速度
D.骑了4分钟时，小明离学校1.2千米 -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABN中，∠B =90°，点M是AB上的动点（不与A,B两点重合），点C是BN延长线上的动点（不与点N重合），且AM=BC，CN=BM，连接CM与AN交于点P.
（1）在图1中依题意补全图形;
（2）小伟通过观察、实验，提出猜想:在点M，N运动的过程中，始终有∠APM=45°.小伟把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的一种思路:
要想解决这个问题，首先应想办法移动部分等线段构造全等三角形，证明线段相等，再构造平行四边形，证明线段相等，进而证明等腰直角三角形，出现45°的角，再通过平行四边形对边平行的性质，证明∠APM=45°.
他们的一种作法是：过点M在AB下方作MD
AB于点M,并且使MD=CN.通过证明△AMD
△CBM,得到AD=CM,再连接DN，证明四边形CMDN是平行四边形，得到DN=CM，进而证明△ADN是等腰直角三角形，得到∠DNA=45°.又由四边形CMDN是平行四边形，推得∠APM=45°.使问题得以解决.请你参考上面同学的思路，用另一种方法证明∠APM=45°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数y＝－x2＋2x，有下列四个结论：①它的对称轴是直线x＝1；②设y1＝－
＋2x1，y2＝－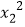
＋2x2，则当x2＞x1时，有y2＞y1；③它的图象与x轴的两个交点是(0，0)和(2，0)；④当0＜x＜2时，y＞0.其中正确结论的个数为( )A. 1 B. 2 C. 3 D. 4
相关试题
