【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(2,2),B(1,0),C(3,1).
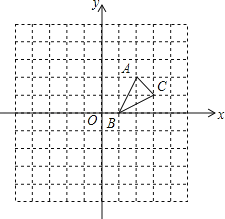
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)画出将△ABC绕原点O按逆时针方向旋转90°所得作的△A2B2C2,并求出C2的坐标;
(3)在旋转过程中,点A经过的路径为弧![]() ,那么
,那么![]() 的长为 ;
的长为 ;
(4)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
参考答案:
【答案】(1)见解析;(2)见解析,(﹣1,3);(3)2![]() ;(4)
;(4)![]() π.
π.
【解析】
试题分析:(1)利用关于x轴对称的点的坐标特征写出点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A2、B2、C2,然后描点即可得到△A2B2C2;
(3)先计算出OA,然后根据弧长公式计算;
(4)观察所画的图形,根据中心对称的定义可判断)△A1B1C1与△A2B2C2成中心对称,然后写出对称中心的坐标.
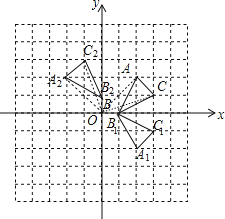
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,并求出C2的坐标为(﹣1,3);
(3)OA=![]() =2
=2![]() ,
,
在旋转过程中,点A经过的路径为弧![]() ,那么
,那么![]() 的长=
的长=![]() =
=![]() π;
π;
(4)△A1B1C1与△A2B2C2成中心对称,对称中心的坐标为(![]() ,
,![]() ).
).
故答案为![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
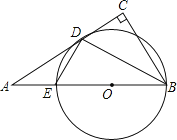
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=
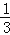 AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.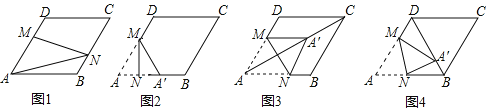
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为200平方米的矩形绿地,并且长比宽多10米,求绿地的长为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=x的解是( )
A.x=1 B.x1=﹣1,x2=1 C.x1=0,x2=1 D.x=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动形式属于旋转的是( )
A.钟表上钟摆的摆动
B.投篮过程中球的运动
C.“神十”火箭升空的运动
D.传动带上物体位置的变化
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的算术平方根是( )
A. 4 B. -2 C. 2 D. ±2
相关试题

