【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
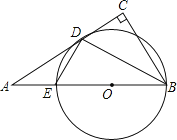
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
参考答案:
【答案】(1)见解析;(2)8.
【解析】
试题分析:(1)连接OD,则有∠1=∠2,而∠2=∠3,得到∠1=∠3,因此OD∥BC,又由于∠C=90°,所以OD⊥AD,即可得出结论.
(2)根据OD⊥AD,则在RT△OAD中,OA2=OD2+AD2,设半径为r,AD=15,AE=9,得到(r+9)2=152+r2,解方程即可.
(1)证明:连接OD,如图所示:
∵OD=OB,
∴∠1=∠2,
又∵BD平分∠ABC,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥BC,
而∠C=90°,
∴OD⊥AD,
∴AC与⊙O相切于D点;
(2)解:∵OD⊥AD,
∴在RT△OAD中,OA2=OD2+AD2,
又∵AD=15,AE=9,设半径为r,
∴(r+9)2=152+r2,
解方程得,r=8,
即⊙O的半径为8.
-
科目: 来源: 题型:
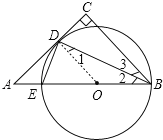
查看答案和解析>>【题目】如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学粗心大意,因式分解时,把等式x4-■=(x2+4)(x+2)(x-▲)中的两个数字弄污了,则式子中的■,▲对应的一组数字可以是( )
A. 8,1 B. 16,2
C. 24,3 D. 64,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形的外角∠DCM的平分线CF于点F.
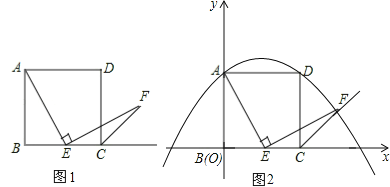
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否一定成立?说出你的理由;
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点,当点E滑动到某处时,点F恰好落在此抛物线上,求此时点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=
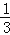 AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.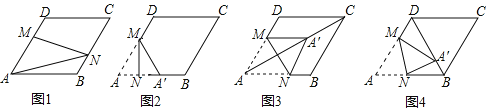
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为200平方米的矩形绿地,并且长比宽多10米,求绿地的长为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(2,2),B(1,0),C(3,1).
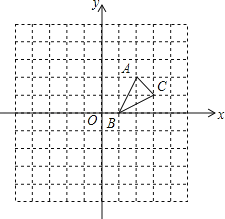
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)画出将△ABC绕原点O按逆时针方向旋转90°所得作的△A2B2C2,并求出C2的坐标;
(3)在旋转过程中,点A经过的路径为弧
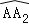 ,那么
,那么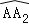 的长为 ;
的长为 ;(4)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
相关试题

