【题目】如图,△ABC中,AB=AC,∠BAC=90°, 
(1)CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,BE的延长线交CA的延长线于M,补全图形,并探究BE和CD的数量关系,并说明理由;
(2)若BC上有一动点P,且∠BPQ= ![]() ∠ACB,BQ⊥PQ于Q,PQ交AB于F,试探究BQ和PF之间的数量关系,并证明你的结论.
∠ACB,BQ⊥PQ于Q,PQ交AB于F,试探究BQ和PF之间的数量关系,并证明你的结论.
参考答案:
【答案】
(1)解:如图1,BE= ![]() CD,理由是:
CD,理由是:
∵BE⊥CD,
∴∠BEC=90°,
∵∠BAC=90°,
∴∠BEC=∠BAC,
∵∠EDB=∠ADC,
∴∠ABM=∠ACD,
∵AB=AC,∠BAM=∠BAC=90°,
∴△ABM≌△ACD,
∴CD=BM,
∵∠MCE=∠BCE,EC=EC,∠BEC=∠MEC=90°,
∴△MEC≌△BEC,
∴BE=EM,
∴BE= ![]() BM=
BM= ![]() CD
CD

(2)解:如图2,BQ= ![]() PF,理由是:
PF,理由是:
作∠ACB的平分线,交BQ延长线于E,交AB于D,
由(1)得:BE= ![]() CD,
CD,
∵∠BPQ= ![]() ∠ACB,∠BCE=
∠ACB,∠BCE= ![]() ∠ACB,
∠ACB,
∴∠BPQ=∠BCE,
∴PQ∥CE,
∴ ![]() =
= ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴BQ= ![]() PF
PF

【解析】(1)如图1,证明△ABM≌△ACD,得CD=BM,再证明△MEC≌△BEC,得BE=EM,则BE= ![]() CD;(2)如图2,根据(1)作辅助线,证明PQ∥EC,得
CD;(2)如图2,根据(1)作辅助线,证明PQ∥EC,得 ![]() ,利用(1)的结论BE=
,利用(1)的结论BE= ![]() CD,得BQ=
CD,得BQ= ![]() PF.
PF.
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数3.645精确到百分位的近似数为( )
A.3.6
B.3.64
C.3.7
D.3.65 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3x2的开口方向是( )
A.向上
B.向下
C.向左
D.向右 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形B,C,E在同一条直线上,连结DC.
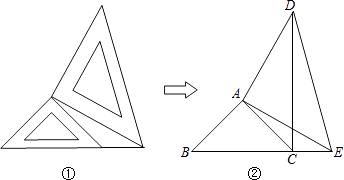
(1)请找出图②中的全等三角形,并给予说明(注意:结论中不得含有未标识的字母);
(2)请判断DC与BE的位置关系,并证明;
(3)若CE=2,BC=4,求△DCE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明住在学校正东方向200米处,从小明家出发向北走150米就到了李华家.若选取李华家为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,则学校的坐标为( )
A. (-150,-200) B. (-200,-150) C. (0,-50) D. (-150,200)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣9=0的根是( )
A.x=3
B.x=﹣3
C.x1=3,x2=﹣3
D.x1=9,x2=﹣9
相关试题

