【题目】已知:如图,菱形花坛ABCD周长是80m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,相交于O点. 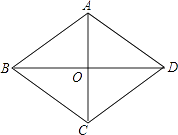
(1)求两条小路的长AC、BD.(结果可用根号表示)
(2)求花坛的面积.(结果可用根号表示)
参考答案:
【答案】
(1)解:∵菱形花坛ABCD周长是80m,∠ABC=60°,
∴AB=BC=DC=AD=20cm,∠ABD=30°,
∴△ABC是等边三角形,
∴AC=20cm,
∴AO=10cm,
∴BO= ![]() =10
=10 ![]() (cm),
(cm),
则BD=20 ![]() cm,AC=20cm
cm,AC=20cm
(2)解:由(1)得:花坛的面积为:20×20 ![]() =400
=400 ![]() (cm2),
(cm2),
答:花坛的面积为400 ![]() cm2
cm2
【解析】(1)直接利用菱形的性质得出△ABC是等边三角形,进而得出AO,BO的长,即可得出答案;(2)利用菱形面积等于对角线乘积的一半即可得出答案.
【考点精析】通过灵活运用菱形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.
-
科目: 来源: 题型:
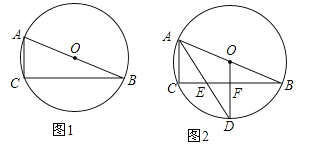
查看答案和解析>>【题目】已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察:
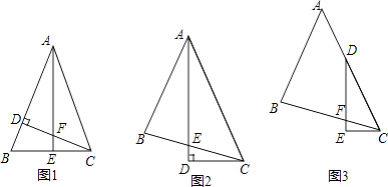
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F. ①写出图1中所有的全等三角形;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E. 求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.

问:
(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次共买进原料和卖出食品各多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.9的平方根为3?
B.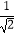 化简后的结果是
化简后的结果是 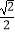
C.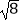 最简二次根式?
最简二次根式?
D.﹣27没有立方根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
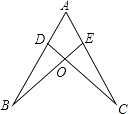
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
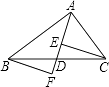
A.1个
B.2个
C.3个
D.4个
相关试题

