【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.求证:
(1)△BAD≌△CAE;
(2)BD⊥CE

参考答案:
【答案】(1)见解析,(2)见解析.
【解析】
(1)要证△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由
∠BAC=∠DAE=90°很易证得;(2)要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.
证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
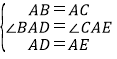 ,
,
∴△BAD≌△CAE(SAS).
(2)BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2020年开始,新冠病毒疫情严峻,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共4000件送往武汉,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用450元购买甲种物品的件数恰好与用400元购买乙种物品的件数相同.
(1)求甲、乙两种救灾物品每件的价格分别是多少元?
(2)经调查,灾区对乙种物品件数需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这4000件物品,需筹集资金多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化难为易.
(1)解方程组
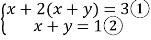
(2)已知
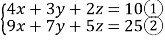 ,求x+y+z的值
,求x+y+z的值解:(1)把②代入①得:x+2×1=3.解得:x=1.
把x=1代入②得:y=0.
所以方程组的解为
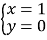 ,
,(2)①×2得:8x+6y+4z=20.③
②﹣③得:x+y+z=5.
(类比迁移)
(1)若
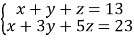 ,则x+2y+3z= .
,则x+2y+3z= .(2)解方程组
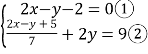
(实际应用)
打折前,买39件A商品,21件B商品用了1080元.打折后,买52件A商品,28件B商品用了1152元,比不打折少花了多少钱?
-
科目: 来源: 题型:
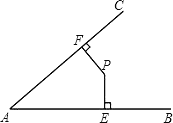
查看答案和解析>>【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
(1)求一次函数和反比例函数的解析式;
(2)结合函数图象,请直接写出
 >ax+b的解集;
>ax+b的解集;(3)若P是x轴上一点,且△ABP的面积是6,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润最多?最多获利是多少元?
相关试题

