【题目】已知点A在平面直角坐标系中第一象限内,将线段AO平移至线段BC,其中点A与点B对应.
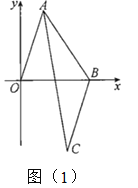
(1)如图(1),若![]()
![]() ,连接AB,AC,在坐标轴上存在一点D,使得
,连接AB,AC,在坐标轴上存在一点D,使得![]() ,求点D的坐标;
,求点D的坐标;
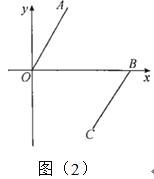
(2)如图(2),若![]() ,点P为y轴上一动点(点P不与原点重合),请直接写出
,点P为y轴上一动点(点P不与原点重合),请直接写出![]() 与
与![]() 之间的数量关系(不用证明).
之间的数量关系(不用证明).
参考答案:
【答案】(1)点D的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;(2)
;(2)![]() 与
与![]() 的数量关系是
的数量关系是![]() 或
或![]() 或
或![]()
【解析】
(1)先根据A,B的坐标找到平移规律,从而求出C的坐标,进而![]() 的面积和
的面积和![]() 的面积可求,则点D的坐标可求;
的面积可求,则点D的坐标可求;
(2)分两种情况讨论:当P在y轴的正半轴上时和当P在y轴的负半轴上时,分情况进行讨论即可.
(1)由线段平移,点![]() 的对应点为
的对应点为![]() ,
,
知线段AO先向石平移2个单位,再向下平移3个单位,
则点![]() 平移后的坐标为
平移后的坐标为![]() ,
,
即![]()
![]() ,
,
![]()
![]()
![]() 点A到x轴的距离为3,到y轴的的距离为1,
点A到x轴的距离为3,到y轴的的距离为1,
若点D在x轴上,
![]()
![]()
![]() 点D的坐标为
点D的坐标为![]() 或
或![]()
若点D在y轴上,
![]()
![]()
∴点D为![]() 或
或![]()
综上所述,点D的坐标为![]() 或
或![]() 或
或![]() 或
或![]()
(2)如图,延长BC交y轴于点E.
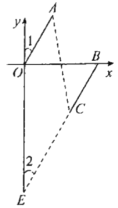
![]() 且
且![]() ,
,
![]() ,
,![]() ,
,
分两种情况讨论:
(1)当P在y轴的正半轴上时,![]()
(2)当P在y轴的负半轴上时,
若P在点E上方(含与点E重台)时,
![]()
即![]()
若P在点E下方时,
![]()
即![]()
综合可得![]() 与
与![]() 的数量关系是
的数量关系是![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
 正方形OABC的边OA、OC在坐标轴上.在
正方形OABC的边OA、OC在坐标轴上.在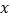 轴上线段
轴上线段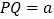 (Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为
(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为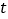 .连接PB,过P作PB的垂线,过Q作
.连接PB,过P作PB的垂线,过Q作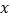 轴的垂线,两垂线相交于点D.连接BD交
轴的垂线,两垂线相交于点D.连接BD交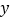 轴于点E,连接PD交
轴于点E,连接PD交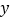 轴于点F,连接PE.
轴于点F,连接PE.(1)求∠PBD的度数.
(2)设△POE的周长为
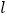 ,探索
,探索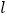 与
与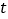 的函数关系式,并写出
的函数关系式,并写出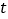 的取值范围.
的取值范围.(3)令
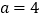 ,当△PBE为等腰三角形时,求△EFD的面积.
,当△PBE为等腰三角形时,求△EFD的面积.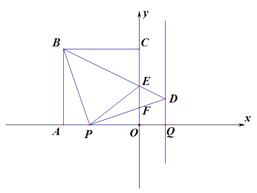
-
科目: 来源: 题型:
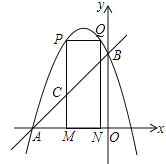
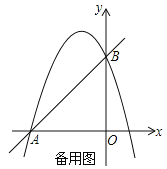
查看答案和解析>>【题目】如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,G是直线AC上一点,F是抛物线上一点,是否存在点G,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=
 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

相关试题

