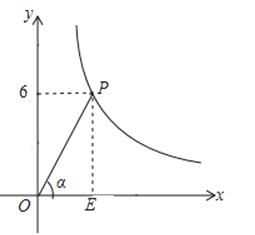
【题目】在平面直角坐标系中,点P(m,6)在第一象限,且P是反比例函数y=![]() (k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
(k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
参考答案:
【答案】解:过点P作PE⊥x轴于点E,则可得PE=6,0E=m,
∵5sin2α﹣7sinα+2.4=0,
∴![]() ,
,
∴![]() 或
或![]() ,
,
当![]() 时,则sinα=
时,则sinα=![]()
∴OP=10,
在RT△POE中,OE=![]() =8,
=8,
∴m=8,此时,k=6×8=48,
∴![]() ;
;
当![]() 时,则sinα=
时,则sinα=![]()
∴OP=![]() ,由勾股定理得:m=
,由勾股定理得:m=![]() ,此时,k=6×4.5=27,
,此时,k=6×4.5=27,
∴![]() .
.
【解析】由5sin2α﹣7sinα+2.4=0,变形为![]() , 从而得出
, 从而得出![]() 或
或![]() ;过点P作PE⊥x轴于点E,则可得PE=6,0E=m,在Rt△POE中根据
;过点P作PE⊥x轴于点E,则可得PE=6,0E=m,在Rt△POE中根据![]() 或
或![]() , 求出OP,继而根据勾股定理求得m的值,然后根据待定系数法即可求得反比例函数的解析式.
, 求出OP,继而根据勾股定理求得m的值,然后根据待定系数法即可求得反比例函数的解析式.
【考点精析】根据题目的已知条件,利用反比例函数的性质的相关知识可以得到问题的答案,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
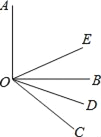
查看答案和解析>>【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(3a2b﹣ab2)﹣2(a2b+2ab2)其中a=﹣2,b=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于代数式3x3y﹣2x2y2+5xy3﹣1,下列说法不正确的是( )
A.它按y的升幂排列
B.它按x的降幂排列
C.它的常数项是﹣1
D.它是四次四项式 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统汁后?将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5
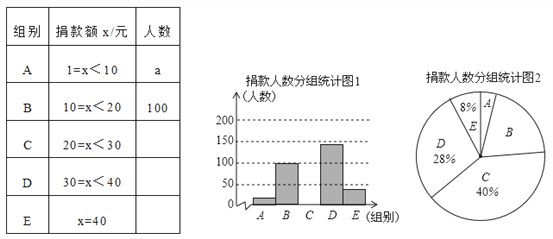
请结合以上信息解答下列问题.
(1)a=______________,本次调查样本的容量是______________________;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)若任意抽出1名学生进行调查,恰好是捐款数不少于30元的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是
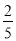 ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为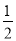
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式按字母x的降幂排列的是( )
A.﹣5x2﹣x2+2x2
B.ax3﹣2bx+cx2
C.﹣x2y﹣2xy2+y2
D.x2y﹣3xy2+x3﹣2y2
相关试题

