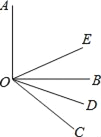
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
参考答案:
【答案】(1)45° ;(2)![]() α;(3)∠DOE的大小与∠BOC的大小无关.
α;(3)∠DOE的大小与∠BOC的大小无关.
【解析】试题分析:(1)首先计算出∠AOC的度数,然后再根据角平分线的性质可得∠COE=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
(2)方法与(1)相同,首先计算出∠AOC的度数,然后再根据角平分线的性质可得∠COE=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
(3)根据(1)(2)的结果可得∠DOE的大小与∠BOC的大小无关.
试题解析:(1)∵∠AOB=90°,∠BOC=38°
∴∠AOC=∠AOB+∠BOC=90°+38°=128°
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×128°=64°
×128°=64°
∠COD=![]() ∠BOC=
∠BOC=![]() ×38°=19°
×38°=19°
∴∠DOE=∠COE﹣∠COD=64°﹣19°=45°
(2)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (α+β)
(α+β)
∠COD=![]() ∠BOC=
∠BOC=![]() β
β
∴∠DOE=∠COE﹣∠COD=![]() (α+β)﹣
(α+β)﹣![]() β=
β=![]() α+
α+![]() β﹣
β﹣![]() =
=![]() α;
α;
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角的度数是26°45′,则这个角的余角为__°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将菱形ABCD放置在平面直角坐标系中,已知A(0,3).B(﹣4,0)
(1)求经过点C的反比例函数解析式;
(2)设P是(1)中所求函数图象上的一点,以P、O、A为顶点的三角形的面积与△COD的面积相等,求点P的坐标.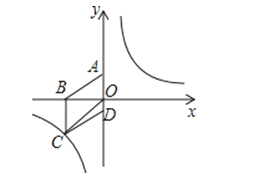
-
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺为1:800000的“中国政区”地图上,量得甲市与乙市之间的距离是2.5cm,则这两市之间的实际距离为( )km.
A.20000000B.200000C.200D.2000000
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(3a2b﹣ab2)﹣2(a2b+2ab2)其中a=﹣2,b=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于代数式3x3y﹣2x2y2+5xy3﹣1,下列说法不正确的是( )
A.它按y的升幂排列
B.它按x的降幂排列
C.它的常数项是﹣1
D.它是四次四项式 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(m,6)在第一象限,且P是反比例函数y=
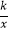 (k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
(k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
相关试题

