【题目】已知数轴上![]() 、
、![]() 两点对应数分别为
两点对应数分别为![]() 和
和![]() ,
, ![]() 为数轴上一动点,对应数为
为数轴上一动点,对应数为![]() .
.
(1)若![]() 为线段
为线段![]() 的三等分点,求
的三等分点,求![]() 点对应的数;
点对应的数;
(2)数轴上是否存在点![]() ,使
,使![]() 点到
点到![]() 点、
点、![]() 点距离和为
点距离和为![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
(3)若![]() 点、
点、![]() 点和
点和![]() 点(
点(![]() 点在原点)同时向左运动,它们的速度分别为
点在原点)同时向左运动,它们的速度分别为![]() 、
、![]() 、
、![]() 个长度单位/分,则第几分钟时,
个长度单位/分,则第几分钟时, ![]() 为
为![]() 的中点?
的中点?
参考答案:
【答案】(1)![]() 或
或![]() (2)10(3)2
(2)10(3)2
【解析】试题分析:(1)根据题意结合图形即可解决问题;
(2)分点P在线段AB的左边或右边两种情况来解答,列出方程即可解决问题.
(3)根据三点的运动速度,准确表示出某一时刻三点对应的数,列出方程即可解决问题.
试题解析:(1)因为AB=4-(-2)=6, ![]() 为线段
为线段![]() 的三等分点,所以
的三等分点,所以![]() 或
或![]() ;
;
![]()
(2)因为距离之和为10,所以P在线段AB外, PA=|x-4|,PB=|-2-x|,
当P在B点右侧时,x>4,则有x-4+x+2=10,解得,x=6;
当P在A点左侧时,x<-2,则有4-x+(-2)-x=10,解得x=-4;
综上,当![]() 或
或![]() 时,
时, ![]()
(3)设![]() 分钟后,
分钟后, ![]() 为
为![]() 的中点,
的中点, ![]() 、
、![]() 、
、![]() 运动
运动![]() 分钟后对应的数分别为
分钟后对应的数分别为![]() ,
, ![]() ,
, ![]() ,
,
由![]() ,得
,得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣8x的顶点坐标为( )
A.(4,16)
B.(﹣4,16)
C.(4,﹣16)
D.(﹣4,﹣16) -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.

(2)四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(3)平面上有
 条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的
条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的 条直线分一个平面所成的区域最多,记为
条直线分一个平面所成的区域最多,记为 ,试研究
,试研究 与
与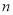 之间的关系.
之间的关系.思维方法天地
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线
 上,点
上,点 在
在 、
、 两点之间,点
两点之间,点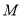 为线段
为线段 的中点,点
的中点,点 为线段
为线段 的中点.若
的中点.若 ,且
,且 使关于
使关于 的方程
的方程 有无数个解.
有无数个解.(1)求线段
 的长;
的长;(2)试说明线段
 的长与点
的长与点 在线段
在线段 上的位置无关;
上的位置无关;(3)如图,若点
 为线段
为线段 的中点,点
的中点,点 在线段
在线段 的延长线上,试说明
的延长线上,试说明 的值不变.
的值不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab

D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab

-
科目: 来源: 题型:
查看答案和解析>>【题目】用直尺和圆规作一个角等于已知角的示意图如右,则说明∠A′O′B′=∠AOB的依据是( )

A. SSS B. SAS C. ASA D. AAS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且(a+b-3)2+|a-2b|=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)线段AO与线段AB的数量关系是______(填“>”、“≥”、“≤”、“<”或“=”);
(2)求证:△AOC≌△ABD;
(3)若∠CAD=30
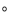 ,当点C运动时,点P在y轴上的位置是否发生改变,为什么?
,当点C运动时,点P在y轴上的位置是否发生改变,为什么?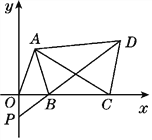
相关试题

