【题目】抛物线y=x2﹣8x的顶点坐标为( )
A.(4,16)
B.(﹣4,16)
C.(4,﹣16)
D.(﹣4,﹣16)
参考答案:
【答案】C
【解析】解: ∵y=x2﹣8x=(x﹣4)2﹣16,
∴抛物线顶点坐标为(4,﹣16),
故选C.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P( 2,-3 )关于x轴的对称点是( )
A. (-2, 3 ) B. (2,3) C. (-2, 3 ) D. (2,-3 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线
y=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元/件。试营销阶段发现:当销售单价25元/件时,每天的销售量是250件;销售单价每上涨1元,每天的销售量就减少10件。
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式。
(2)求销售单价为多少元时,该文具每天的销售利润最大?
(3)商场的营销部结合上述情况,提出了A,B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元。
请比较哪种方案的最大利润更高,并说明理由。(本题12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.

(2)四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(3)平面上有
 条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的
条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的 条直线分一个平面所成的区域最多,记为
条直线分一个平面所成的区域最多,记为 ,试研究
,试研究 与
与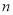 之间的关系.
之间的关系.思维方法天地
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线
 上,点
上,点 在
在 、
、 两点之间,点
两点之间,点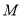 为线段
为线段 的中点,点
的中点,点 为线段
为线段 的中点.若
的中点.若 ,且
,且 使关于
使关于 的方程
的方程 有无数个解.
有无数个解.(1)求线段
 的长;
的长;(2)试说明线段
 的长与点
的长与点 在线段
在线段 上的位置无关;
上的位置无关;(3)如图,若点
 为线段
为线段 的中点,点
的中点,点 在线段
在线段 的延长线上,试说明
的延长线上,试说明 的值不变.
的值不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上
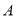 、
、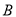 两点对应数分别为
两点对应数分别为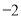 和
和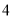 ,
, 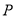 为数轴上一动点,对应数为
为数轴上一动点,对应数为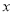 .
.(1)若
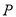 为线段
为线段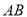 的三等分点,求
的三等分点,求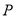 点对应的数;
点对应的数;(2)数轴上是否存在点
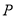 ,使
,使 点到
点到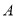 点、
点、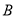 点距离和为
点距离和为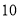 ?若存在,求出
?若存在,求出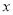 值;若不存在,请说明理由.
值;若不存在,请说明理由.(3)若
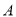 点、
点、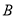 点和
点和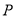 点(
点(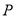 点在原点)同时向左运动,它们的速度分别为
点在原点)同时向左运动,它们的速度分别为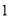 、
、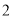 、
、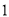 个长度单位/分,则第几分钟时,
个长度单位/分,则第几分钟时, 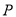 为
为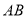 的中点?
的中点?
相关试题

