【题目】下列命题中,(1)数轴上的所有点都表示有理数;(2)无理数可以用数轴上的点表示;(3)实数与数轴上的点一一对应;(4)无限小数是无理数;(5)带根号的数都是无理数;(6)数轴上的点不是表示有理数,就是表示无理数;错误命题的个数是( )
A.1B.2C.3D.4
参考答案:
【答案】C
【解析】
所有实数都可以用数轴上的点表示,数轴上所有的点都表示实数,实数分为有理数和无理数;无限不循环小数是无理数,无限循环小数是有理数,根据以上内容判断即可.
解:∵实数与数轴上的点一一对应,实数分为有理数与无理数,所有有理数和无理数都可以用数轴上的点表示,∴(1)错误;(2)(3)(6)正确;
∵无限不循环小数是无理数,无限循环小数是有理数,∴(4)错误;
带根号的数不一定都是无理数,如![]() =2,
=2,![]() 是有理数,不是无理数,∴(5)错误;
是有理数,不是无理数,∴(5)错误;
∴错误的是(1)(4)(5).
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(a,4)(其中a<-3),射线OA与反比例函数
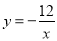 的图象交于点P,点B,C分别在函数
的图象交于点P,点B,C分别在函数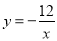 的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.(1)当a=-6,求线段AC的长;
(2)当AB=BO时,求点A的坐标;
(3)求证:
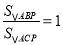 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宝安区的某商场经市场调查,预计一款夏季童装能获得市场青睐,便花费 15000 元购进了一批此款童装,上市后很快售罄.该店决定继续进货,由于第二批进货数量是第一批进货数量的 2 倍,因此单价便宜了 10 元,购进第二批童装一共花费了 27000 元.
(1)该店所购进的第一批童装的单价是多少元?
(2)两批童装按相同标价出售,经理根据市场情况,决定对第二批剩余的 100 件打七折销售.若两批童装全部售完后,利润不低于 30%,那么每件童装标价至少是多少元?
-
科目: 来源: 题型:
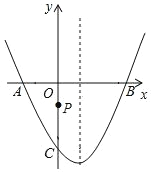
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数 y=ax2+bx+c 的图象交 x 轴于A、B 两点,交 y 轴于 C 点,P 为 y 轴上的一个动点,已知 A(﹣2,0)、C(0,﹣2
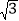 ),且抛物线的对称轴是直线 x=1.
),且抛物线的对称轴是直线 x=1.(1)求此二次函数的解析式;
(2)连接 PB,则
 PC+PB 的最小值是 ;
PC+PB 的最小值是 ;(3)连接 PA、PB,P 点运动到何处时,使得∠APB=60°,请求出 P 点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形 OABC,O 为坐标原点,已知 A(4,0)、C(0,2),D 为边 OA 的中点,连接 BD,M 点与 C 点重合,N 为 x 轴上一点,MN∥BD, 直线 MN 沿着 x 轴向右平移.
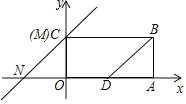
(1)当四边形 MBDN 为菱形时,N 点的坐标是 ;
(2)当 MN 平移到何处时,恰好将四边形 ODBC 的面积为 1:3 的两部分?请求出此时直线 MN 的解析式;
(3)在(1)的条件下,在矩形 OABC 的四条边上,是否存在点 F,连接 DF, 将矩形沿着 DF 所在的直线翻折,使得点 O 恰好落在直线 MN 上,若存在, 求出 F 点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
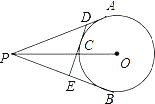
查看答案和解析>>【题目】如图,PA、PB切⊙O于A.B,点C在AB上,DE切⊙O于C,交PA、PB于D.E,已知PO=5cm,⊙O的半径为3cm,则△PDE的周长是______.
-
科目: 来源: 题型:
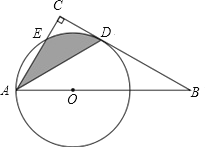
查看答案和解析>>【题目】如图,∠C=90°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠BAC=60°,OA=1,求阴影部分的面积(结果保留π).
相关试题

