【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 . 
参考答案:
【答案】![]()
【解析】解:∵点A的坐标为(1,0),点D的坐标为(0,3),
∴OA=1,OD=3,
∵∠AOD=90°,
∴AD= ![]() =
= ![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=AD= ![]() ,
,
∴∠ODA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴ ![]() ,即
,即 ![]() ,解得:BA1=
,解得:BA1= ![]() ,
,
∴CA1= ![]() ,
,
同理,可得:C1A2= ![]() ,
,
∴第4个正方形的边长为 ![]() =
= ![]() ,
,
故答案为: ![]() .
.
先利用勾股定理求出AD的长,根据正方形的性质,可得出AB、BC的长。再证明△ABA1∽△DOA,求出CA1的长,按同样的方法求出C1A2的长、C2A3的长,观察规律得出第4个正方形的边长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.求足球和篮球的单价各是多少元?
-
科目: 来源: 题型:
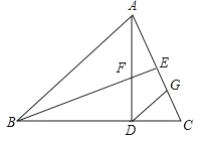
查看答案和解析>>【题目】如图,在
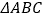 中,
中,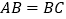 ,
,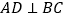 于点
于点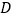 ,点
,点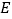 为
为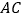 中点,连接
中点,连接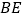 交
交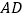 于点
于点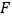 ,且
,且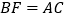 ,过点
,过点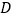 作
作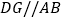 ,交
,交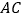 于点
于点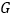 .
.求证:(1)

(2)
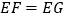 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 是等边三角形
是等边三角形 边
边 上一动点(点
上一动点(点 )与点
)与点 不重合,连接
不重合,连接 ,以
,以 为边在
为边在 上方作等边三角形
上方作等边三角形 ,连接
,连接 ,你能发现
,你能发现 与
与 之间的数量关系吗?并证明你发现的结论.
之间的数量关系吗?并证明你发现的结论.(2)如图二,当动点
 在等边三角形
在等边三角形 边
边 上运动时(点
上运动时(点 与点
与点 不重合),连接
不重合),连接 ,以
,以 为边在其上方、下方分别作等边三角形
为边在其上方、下方分别作等边三角形 和等边三角形
和等边三角形 ,连接
,连接 ,
, ,探究
,探究 ,
, 与
与 有何数量关系?并证明你探究的结论.
有何数量关系?并证明你探究的结论.(3)如图三,当动点
 在等边三角形
在等边三角形 边
边 的延长线上运动时,其他作法与图2相同,若
的延长线上运动时,其他作法与图2相同,若 ,请直接写出
,请直接写出 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y=
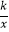 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 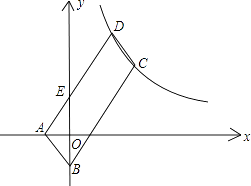
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+(m+2)x+
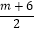 与x轴交于A(﹣2﹣n,0),B(4+n,0)两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A(﹣2﹣n,0),B(4+n,0)两点(A在B的左侧),与y轴交于点C,顶点为D.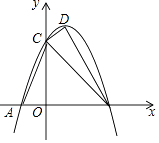
(1)求此抛物线的解析式;
(2)以点B为直角顶点作直角三角形BCE,斜边CE与抛物线交于点P,且CP=EP,求点P的坐标;
(3)将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转的角度为α,旋转后的图形为△BO′C′.当旋转后的△BO′C′有一边与BD重合时,求△BO′C′不在BD上的顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//CD,点G在直线AB上, 点H在直线CD上,点K在AB、CD之间且在G、H所在直线的左侧, 若 ∠GKH=60°,点P为线段KH上一点(不和K、H重合),连接PG并延长到M, 设∠KHC=n∠KGP,要使得
 为定值,则n=_____
为定值,则n=_____
相关试题

