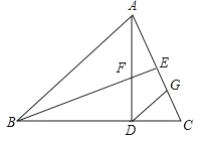
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
求证:(1)![]()
(2)![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)只要证明△BDF≌△ADC,推出BD=AD,推出∠BAD=∠ABD=2∠CBE=2∠DAC即可解决问题.
(2)延长BE、DG交于点K.先证明Rt△AEF≌Rt△KEG,再根据其性质即可得到结论.
证明:(1)∵AD⊥BC,
∴∠ADC=90°
∵AB=BC,E为AC中点,
∴∠ABE=∠CBE=![]() ∠ABC,BE⊥AC,
∠ABC,BE⊥AC,
∴∠BEC=90°,
∴180°-∠C-∠ADC=180°-∠C-∠BEC
即∠CBE=∠CAD,
在△BDF和△ADC中, ,
,
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠BAD=∠ABD=2∠CBE=2∠DAC.
(2)延长BE、DG交于点K.
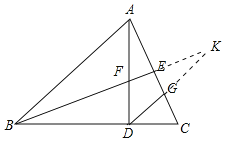
∵DG∥AB,
∴∠CGD=∠CAB,∠K=∠ABE,
∵∠BAC=∠C,
∴∠CGD=∠C
∵∠K=∠CBE=∠CAD
∠AEF=∠KEG=90°,∠EAF=∠EKG,
∴DG=DC,DK=BD,
∴DG=DF,DK=BD=AD,
∴DK-DG=AD-DF,即GK=AF
在Rt△AEF和Rt△KEG中
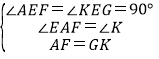 ,
,
∴Rt△AEF≌Rt△KEG (AAS),
∴EF=EG.
-
科目: 来源: 题型:
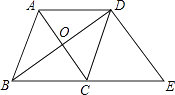
查看答案和解析>>【题目】在菱形ABCD中,对角线AC、BD相交于点O,AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为( )
A.22
B.24
C.48
D.44 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )

A.45°
B.85°
C.90°
D.95° -
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.求足球和篮球的单价各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 是等边三角形
是等边三角形 边
边 上一动点(点
上一动点(点 )与点
)与点 不重合,连接
不重合,连接 ,以
,以 为边在
为边在 上方作等边三角形
上方作等边三角形 ,连接
,连接 ,你能发现
,你能发现 与
与 之间的数量关系吗?并证明你发现的结论.
之间的数量关系吗?并证明你发现的结论.(2)如图二,当动点
 在等边三角形
在等边三角形 边
边 上运动时(点
上运动时(点 与点
与点 不重合),连接
不重合),连接 ,以
,以 为边在其上方、下方分别作等边三角形
为边在其上方、下方分别作等边三角形 和等边三角形
和等边三角形 ,连接
,连接 ,
, ,探究
,探究 ,
, 与
与 有何数量关系?并证明你探究的结论.
有何数量关系?并证明你探究的结论.(3)如图三,当动点
 在等边三角形
在等边三角形 边
边 的延长线上运动时,其他作法与图2相同,若
的延长线上运动时,其他作法与图2相同,若 ,请直接写出
,请直接写出 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y=
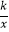 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 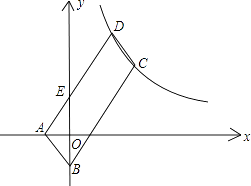
相关试题

