【题目】如图,AB//CD,点G在直线AB上, 点H在直线CD上,点K在AB、CD之间且在G、H所在直线的左侧, 若 ∠GKH=60°,点P为线段KH上一点(不和K、H重合),连接PG并延长到M, 设∠KHC=n∠KGP,要使得![]() 为定值,则n=_____
为定值,则n=_____

参考答案:
【答案】3
【解析】
延长MP交CD于点O,设∠KGP=x,则∠KHC=nx,利用平行线的性质以及三角形外角性质,即可得到∠GPH=60°+x,∠AGM=∠COM=120°+(n-1)x,由![]() 为定值可得n的值.
为定值可得n的值.
解:延长MP交CD于点O,
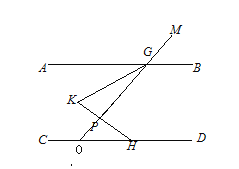
设∠KGP=x,则∠KHC=nx,
∵∠GKH=60°,
∴∠GPH=60°+x,
∠OPH=180°-(60°+x)=120°-x,
∵AB∥CD,
∴∠AGM=∠COM=∠OPH+∠KHC=120°-x+ nx=120°+(n-1)x,
∴![]() =
=![]()
∵n-1=2时,![]() 为定值:
为定值:![]() =
=![]() =2,
=2,
∴n-1=2,n=3.
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y=
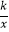 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 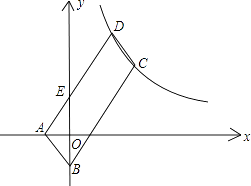
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+(m+2)x+
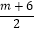 与x轴交于A(﹣2﹣n,0),B(4+n,0)两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A(﹣2﹣n,0),B(4+n,0)两点(A在B的左侧),与y轴交于点C,顶点为D.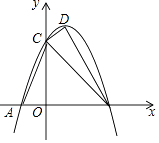
(1)求此抛物线的解析式;
(2)以点B为直角顶点作直角三角形BCE,斜边CE与抛物线交于点P,且CP=EP,求点P的坐标;
(3)将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转的角度为α,旋转后的图形为△BO′C′.当旋转后的△BO′C′有一边与BD重合时,求△BO′C′不在BD上的顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,在Rt△DEF中,∠DFE=90°,EF=6,DF=8,E、F两点在BC边上,DE、DF两边分别与AB边交于点G、H.固定△ABC不动,△DEF从点F与点B重合的位置出发,沿BC边以每秒1个单位的速度向点C运动;同时点P从点F出发,在折线FD﹣DE上以每秒2个单位的速度向点E运动.当点E到达点C时,△DEF和点P同时停止运动.设运动时间为t(秒).

(1)当t=2时,PH=cm,DG=cm;
(2)当t为何值时,△PDG为等腰三角形?请说明理由;
(3)当t为何值时,点P与点G重合?写出计算过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=45°.以AB为直径的⊙O与BC相切于B,交AC于点D,CO的延长线交⊙O于点E,过点作弦EF⊥AB,垂足为点G.

(1)求证:①EF∥CB,②AD=CD;
(2)若AB=10,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明:
已知:AB//CD,连AD交BC于点F,∠1=∠2,求证:∠B+∠CDE=180°
证明:∵∠1= ( )
又∵∠1=∠2
∴∠BFD=∠2( )
∴BC// ( )
∴∠C+ =180°( )
又∵AB//CD
∴∠B=∠C( )
∴∠B+∠CDE=180°

相关试题

